Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 8.1 - Ex. 111
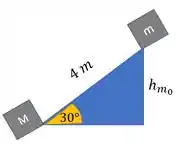
Um bloco de (massa ) e um segundo bloco (massa ) estão inicialmente em repouso sobre um plano inclinado sem atrito. (Figura 8-56). A massa está apoiada sobre uma mola com constante de força igual a . A distância ao longo do plano entre os dois blocos é O bloco de é largado, sofrendo uma colisão elástica com o bloco maior. O bloco de é rebatido, então subindo até uma distância de ao longo do plano inclinado. O bloco de massa atinge um repouso momentâneo a de sua posição inicial. Determine .
Passo 1
Oi, pessoal, tudo bem? Ele dá muita informação para gente né? Vamos começar organizando.
Temos que e queremos saber quando vale .
Inicialmente todo mundo está em repouso. Então se for a velocidade inicial do bloco de massa e a velocidade inicial do bloco de massa , vamos ter:
E a distância entre eles é no plano inclinado. Usando trigonometria a gente consegue descobrir a altura inicial do bloco de massa em relação a altura de :
O bloco de massa é largado e colide elasticamente com o bloco maior. Se a colisão é elástica, a gente pode dizer que houve conservação de energia.
Aí temos uma segunda situação. O bloco menor desce, e aperta o bloco maior contra a mola, que fica com uma deformação adicional de . Nesse momento ambos estão em repouso. Então temos
E depois o bloco de massa sobe a uma distância de no plano inclinado. Aí a altura dele em relação ao bloco maior fica sendo
Usamos o mesmo raciociocínio aqui que usamos para achar . E como essa é altura máxima do bloco depois da colisão, temos .
E mais umas informações adicionais: não temos atrito e a constante da mola é .
Agora vamos ver como achar a partir dessas situações. Bora!
Passo 2
Cara, uma coisa boa que a gente pode fazer é entender o que aconteceu com a energia desses blocos.
Porque como a energia do movimento se conserva por ser uma colisão elástica, o que acontece é que vai haver uma troca de energias. Aí a gente pode usar a equação da conservação de energia.
Bem, inicialmente o bloco de massa tinha uma altura, mas no final na altura dele é menor. Então ele perdeu uma altura , que é o mesmo que perder energia potencial gravitacional dada por
(já que a energia potencial gravitacional é dada por )
Como é menor que , essa variação de energia é negativa, o que caracteriza uma perda, né?
E como as velocidades inicial e final do bloco são nulas, não teve variação de energia cinética.
Passo 3
Agora vamos pensar no que aconteceu com o bloco maior de massa . Inicialmente ele estava paradão. Aí na colisão ele recebeu a energia perdida pelo bloco . O que essa energia fez com ele?
Bem, essa energia foi capaz de aumentar a deformação da mola de . E isso gera um aumento de energia potencial elástica do bloco de
(positiva porque é aumento de energia)
Maaas, como a mola deforma , o bloco desce essa distância no plano inclinado, então há aí uma perda energia potencial gravitacional também. A perda de altura dada pelo movimento de na rampa vai ser
(mesmo raciocício de achar , tá?)
E essa perda de altura causa uma perda de energia potencial gravitacional:
Percebe que o sinal de negativo da perda vem exatamente da variação negativa de altura.
E novamente não temos variação de energia cinética porque o bloco fica em repouso na posição de deformação nova da mola.
Passo 4
A conservação de energia do sistema diz que a energia total do sistema não muda. Então a variação de energia no sistema é nula.
Só que essa variação é a soma de todas as variações que a gente achou:
Substituindo a expressão de cada uma, temos:
Resolvendo para , temos:
Substituindo os dados: