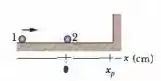
Na Fig. 9-66, a partícula 1, de massa , desliza para a direita ao longo de um eixo em um piso sem atrito com uma velocidade escalar de . Quando chega ao ponto , sofre uma colisão elástica unidimensional com a partícula 2 de massa , inicialmente em repouso. Quando a partícula 2 se choca com uma parede no ponto , ricocheteia sem perder velocidade escalar. Em que ponto do eixo a partícula 2 volta a colidir com a partícula 1?

Oi, galerinha! Tudo bom? Para resolver essa questão vamos olhar precisamente para o momento da colisão entre as duas partículas, onde e . Usando as leis de conservação de energia e do momento linear.

Aplicando para a partícula 1,

Isolando a velocidade final de 1,

Agora vamos olhar para partícula 2

A uma velocidade de a partícula leva para percorrer uma distância e voltar ao ponto. Nesse instante, a partícula 1 se encontra no ponto