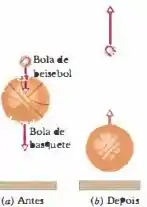
Uma pequena esfera de massa está verticalmente acima de uma bola maior de massa (com uma pequena separação, como no caso das bolas de beisebol e basquete da Fig.9 -68a) e as duas bolas são deixadas cair simultaneamente de uma altura . (Suponha que os raios das bola são desprezíveis em comparação com .) (a) Se a bola maior ricocheteia elasticamente no chão e depois a bola menor ricocheteia elasticamente na maior, que valor de faz com que a bola maior pare momentaneamente no instante em que colide com a menor? (b) Nesse caso, que altura atinge a bola menor (Fig. 9-68b)?

Bom pessoal , a colisão da bola maior com o chão é uma colisão elástica de um objeto leve com um objeto de massa muito maior, na qual a velocidade do objeto leve muda de sentido conservando o mesmo módulo. Assim, imediatamente após a colisão, a bola maior começa a subir com uma velocidade escalar enquanto a bola menor ainda está descendo com a mesma velocidade escalar. Para calcularmos a velocidade da bola maior após a colisão podemos usar a fórmula :

De acordo com a equação acima, para que a velocidade da bola maior seja nula no momento da colisão, devemos ter Como , .

Usamos a mesma equação (intercambiando e ) para calcular a velocidade da bola menor imediatamente após a colisão:

o que nos dá, para , . Para calcular a altura atingida pela bola menor, usamos a lei de conservação da energia. A energia cinética inicial é , a energia potencial inicial é zero, a energia cinética final é zero e a energia potencial final é . Assim,

Para , obtemos .