Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 15.1 - Ex. 23
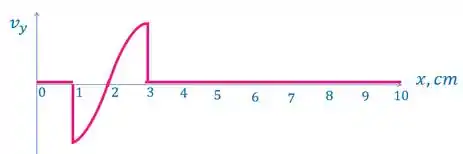
Faça um esboço da velocidade de cada segmento da corda em função da posição, para o pulso mostrado na Figura 15-30
Passo 1
Olá, querido! Então, ele pede o esboço da velocidade de cada segmento da corda em função da posição .
Como assim? Ele quer a velocidade instantânea de cada pedacinho de corda nesse instante mostrado no gráfico que ele deu.
Basicamente é a velocidade com que um pontinho da corda desce (nesse caso a velocidade é negativa) ou sobe (nesse caso ela é positiva), por isso vamos chama-la de . É uma velocidade vertical.
Beleza, mas como a gente vai achar esse num gráfico de posição por altura ? Cara, a gente vai usar a nossa imaginação e ver como a posição de cada pontinho da corda variou no tempo, ou seja, logo depois de (instante mostrado no gráfico).
Vamos!
Passo 2
Vamos refletir primeiro sobre os pontos da corda que forma o pulso, tudo bem?
Esse pulso se move para a direita, certo? Isso quer dizer que a parte da corda que está antes do pico do pulso tende a descer e a parte da corda que está depois do pico tende a subir.
Aí você lembra que a velocidade descreve a direção e sentido do movimento. Então se nesse instante, um ponto da corda está subindo, ele tem velocidade instantânea para cima, e se ele está descendo, a velocidade instantânea está para baixo. Ok até aqui?
Falta só mais uma coisinha. Antes do pico a velocidade instantânea é negativa e depois dele é positiva. Se a velocidade passou de negativa para positiva, quer dizer que em algum ponto intermediário a velocidade instantânea foi nula. Onde acontece isso? No pico!
Então a velocidade no pico é nula. Outra coisa que percebemos aí é que quanto mais perto do pico, menor é a velocidade em módulo, porque ela se aproxima do zero, tudo bem?
Agora olhando para o resto da corda, temos que não há tendencias de movimento a não ser em pontinhos muuuito próximos do pulso, logo a gente pode considerar que fora do pulso.
Passo 3
Juntando a analise que fizemos acima, temos o seguinte:
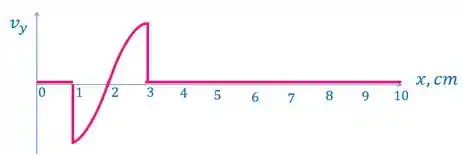
Repara que quanto mais perto de , mais a velocidade é menor em módulo. Repara também que temos um salto de velocidade em e , porque esses são o começo e o final do pulso respectivamente, e logo antes e logo depois dele a velocidade é nula.
Resposta
