Um bloco de está viajando para a direita (sentido ) a , e um segundo bloco de está viajando para a esquerda a.
Determine a energia cinética total dos dois blocos.
Determine a velocidade do centro de massa do sistema de dois blocos.
Determine a velocidade de cada bloco em relação ao centro de massa.
Determine a energia cinética dos blocos em relação ao centro de massa.
Mostre que a resposta para a parte é maior do que a resposta da parte por uma quantidade igual à energia cinética associada ao movimento do centro de massa.
Passo 1
Olá, querido! Cê está bem?
Temos dois blocos viajando com velocidades contrárias. Primeiro, vamos definir como o sentido positivo do eixo para a direita.
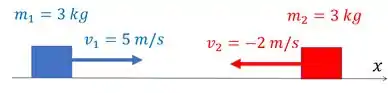
Agora podemos entrar nos itens e responder cada um. Bora lá!
Passo 2
A energia cinética total do sistema é a soma das energias cinéticas de cada bloco:
Aí a gente substitui a expressão da energia cinética para cada caso:
Substituindo as variáveis pelos correspondentes valores numéricos:
Passo 3
A gente quer a velocidade do centro de massa do sistema formado pelos dois blocos. Como não há menção de forças externas sobre eles, a gente pode usar a lei da conservação de quantidade de movimento:
Onde é a massa total do sistema, ou seja, a soma das massas de cada bloco:
representa a soma das quantidades de movimento de cada bloco. A quantidade de movimento é dada por , então essa soma para o nosso caso fica:
E é a velocidade do centro de massa do sistema que gente quer achar. Então vamos substituir e na lei da conservação:
Isolando
e substituindo os valores numéricos na equação acima (lembrando que a é negativo porque viaja no sentido contrário ao eixo positivo):
Obs: estamos trabalhando com as velocidades como grandezas vetoriais, por isso a gente coloca esse vetor unitário , já que nosso movimento está acontecendo na direção ;
Passo 4
Ele quer uma velocidade relativa. A velocidade relativa de um bloco em relação ao centro de massa.
Para achar uma velocidade relativa, a gente monta a equação de velocidade relativa. Para o nosso caso fica:
E o que ela quer dizer? Quer dizer que a velocidade do bloco em relação ao solo é igual a soma da velocidade do bloco relativa ao centro de massa do sistema com a velocidade do centro de massa em relação ao solo .
Aí para achar a velocidade relativa de um bloco em relação ao centro de massa, a gente precisa isolar da nossa equação:
Temos a velocidade de cada bloco e a do centro de massa. Vamos então substituir os valores numéricos para cada bloco, de modo que possamos obter a velocidade relativa de cada um deles:
Para o segundo bloco:
Passo 5
Ele quer a energia cinética dos blocos em relação ao centro de massa. Então o que a gente vai fazer é calcular a energia cinética de cada bloco e somar.
Só que como a gente quer a energia em relação ao centro de massa, vamos usar as velocidades relativas ao centro de massa que a gente calculou no item anterior. Fica assim:
Substituindo os valores numéricos e calculando :
Passo 6
A energia cinética do centro de massa é dada por:
Ou seja, a gente usa a fórmulinha da energia cinética, mas a massa vai ser a massa total do sistema e a velocidade é a velocidade do centro de massa.
Substituindo os valores numéricos e calculando :
A energia cinética do centro de massa é igual a diferença entre as energias obtidas nas letras e , como vemos no cálculo abaixo:
E isso era o que ele queria que a gente provasse!
Resposta
(para a direita) e (para a esquerda)