Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 8.1 - Ex. 37

Uma bomba de massa m e rapidez v explode e se parte em dois fragmentos iguais. Se a bomba estava se movendo horizontalmente em relação à Terra, e um dos fragmentos está, em seguida à explosão, se movendo verticalmente para cima com rapidez v , determine a velocidade v → ' do outro fragmento imediatamente após a explosão.

Passo 1

Oláaaa, cê tá bem?

Então, a gente tem uma bomba que se divide em duas partes.

Para começar, vamos definir como sentido positivo do eixo x , o sentido da bomba ligeiramente antes da explosão. Nosso esqueminha:

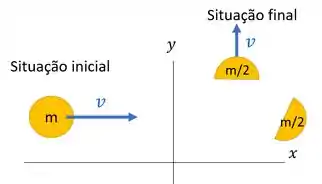
Temos dois momentos. Na situação inicial (1), temos a bomba de massa m com rapidez na direção positiva de x , então sua velocidade é:

v → b o m b a = v i ^

E depois, no segundo momento (2), temos um fragmento de massa m / 2 (já que a bomba se divide em duas), com rapidez v para cima. Logo a velocidade dele é

v → f r a g m e n t o . 1 = v j ^

E nesse mesmo momento temos também um segundo fragmento de massa m / 2 . Mas não sabemos sua velocidade. É exatamente isso que o enunciado nos pergunta! Então vamos descobrir v → f r a g m e n t o . 2 = v → ' . Bora!

Passo 2

Temos dois momentos, a massa e as velocidades das partículas. Isso é uma super dica para a gente aplicar a conservação de momento linear para relacionar as massas dos fragmentos com suas respectivas velocidades:

p → i =   p → f

O momento linear é dado pelo produto entre velocidade da partícula e massa. p → i é o momento da bomba só, e vale:

p → i = m v → b o m b a = m v i ^

p → f é a soma dos momentos dos dois fragmentos (o momento total da segunda situação):

p → f = m 2 v → f r a g m e n t o . 1 + m 2 v → f r a g m e n t o . 1

Substituindo as expressões que temos para essas velocidades até agora:

p → 2 = 1 2 m v j ^ +   1 2 m v → '

Substituindo p → i e p → f   na nossa equação da conservação:

p → i =   p → f

m v i ^ =   1 2 m v j ^ +   1 2 m v → '

Onde v → ' é a velocidade pedida do nosso fragmento.

Passo 3

Somando vetorialmente membro a membro e cancelando as massas m , encontramos que:

2 m v i ^ =   m v j ^ +   m v → '

2 v i ^ =   v j ^ +   v → '

Isolando v → '

v → ' = 2 v i ^ - v j ^

Resposta

A velocidade v → ' do segundo fragmento da bomba era:

v → ' = 2 v i ^ - v j ^

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um projétil de 3,00 k g é disparado com uma rapidez inicial de 120 m / s a um ângulo de 30 ° com a horizontal. No topo de sua trajetória, o projetil explode e se divide em dois fragmentos, de masses 1
Em jogos de hóquei, os discos são guardados no congelador, antes do jogo, para serem mais facilmente manejados. (a) Explique por que discos à temperatura ambiente seriam mais difíceis de manejar com a
Para manter os registros de recordes consistentes, de ano para ano, as associações de beisebol checam, aleatoriamente, o coeficiente de restituição entre novas bolas de beisebol e superfícies de madei
Verdadeiro ou falso:A quantidade de movimento linear total de um sistema pode ser conservada mesmo quando a energia mecânica do sistema não o é.Para que a quantidade de movimento linear total de um si
Mostre que, se duas partículas têm a mesma energia cinética, então as magnitudes de suas quantidades de movimento são iguais apenas se elas têm a mesma massa.