Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 121

Um bloco de 45   k g desliza para baixo, em um plano inclinado que forma um ângulo de 28 ° com a horizontal. Partindo do repouso, o bloco desliza uma distância de 2,4   m em 5,2   s . Encontre o coeficiente de atrito cinético entre o bloco e o plano.

Passo 1

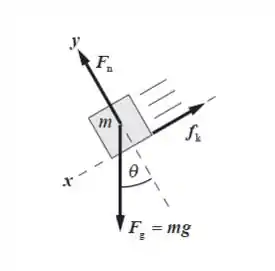
As forças que agem sobre o bloco, uma vez que desliza para baixo, são mostradas no diagrama corpo livre abaixo. A aceleração do bloco pode ser determinada a partir das informações de distância e tempo dadas no problema. A aplicação da Segunda lei de Newton para o bloco levará a uma expressão para o coeficiente de atrito cinético em função da aceleração do bloco e do ângulo de inclinação.

Passo 2

Aplicando a Segunda Lei de Newton no eixo x:

∑ F x = m g s e n θ - f k = m a x

E no eixo y, lembrando que o bloco não sobe nem desce no eixo y, pois ele está sempre em contato com o bloco:

∑ F y = F n - m g c o s θ = 0 ⇒ F n = m g c o s θ

Da definição de força de atrito cinético, temos:

f k = μ k F n ⇒ μ k m g c o s θ

Passo 3

Substituindo essa última equação na primeira do passo 2, temos:

m g s e n θ - μ k m g c o s θ = m a x ⇒ μ k = g s e n θ - a x g c o s θ

Usando a equação horária do espaço:

Δ x = v 0 x Δ t + 1 2 a x Δ t 2

Considerando a velocidade inicial v 0 x = 0 :

Δ x = 1 2 a x Δ t 2 ⇒ a x = 2 Δ x Δ t 2

Passo 4

Substituindo a expressão de a x na equação anterior:

μ k = g s e n θ - 2 Δ x Δ t 2 g c o s θ

Substituindo pelos valores numéricos:

μ k = 9,81 m s 2 s e n 28 ° - 2 2,4   m 5,2   s 2 9,81 m s 2 c o s 28 ° = 0,51

Resposta

μ k = 0,51

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um jogador desliza no campo, após uma tentativa de alcançar a bola. Supondo valores razoáveis para a distância percorrida e a rapidez do jogador antes e após a escorregada, estime a força média de atr
Um caminhão viaja ao longo de uma estrada horizontal reta, carregando vários objetos. Se o caminhão está aumentando sua rapidez, quais são as forças que, atuando sobre os objetos, também fazem com que
Blocos feitos do mesmo material, mas de diferentes tamanhos, são transportados por um caminhão que está se movendo ao longo de uma estrada horizontal reta. Todos os blocos deslizarão se a aceleração d
Um bloco de massa m repousa sobre um plano inclinado em um ângulo de θ com a horizontal. Segue-se que o coeficiente de atrito estática entre o bloco e o plano é(a) μ e ≥ g (b) μ e = t a n θ (c) μ e ≤
Um bloco de massam repousa sobre um plano inclinado em um ângulo de 30 ° com a horizontal, como mostra a figura abaixo. Quais das seguintes alternativas sobre a magnitude da força de atrito estático f