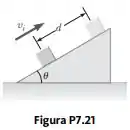
Um bloco de 5,00 kg é colocado em movimento para cima em um plano inclinado com velocidade inicial de vi = 8,00 m/s (Fig. P7.21). O bloco chega ao repouso depois de percorrer d = 3,00 m ao longo do plano, que é inclinado a um ângulo de θ = 30,0º com a horizontal. Para esse movimento, determine (a) a variação na energia cinética do bloco, (b) a variação na energia potencial do sistema bloco-Terra e (c) a força de atrito exercida sobre o bloco (presumida constante). (d) Qual é o coeficiente de atrito cinético?

(b)A variação da energia potencial gravitacional é dada por:

Onde e são as alturas, final e inicial, do bloco, em relação à Terra.

A gente não conhece o valor pra , mas como a diferença é em relação à Terra, a gente pode considerar como referência de ponto de partida ou seja, vale que .

Com isso, a gente pode reescrever assim:

Beleza, mas agora falta calcular . Isso a gente vai fazer por trigonometria!

Olha só, se o bloco se deslocou, pra cima, por , no lado da rampa que equivale à hipotenusa do triângulo retângulo (marcado em vermelho), naturalmente ele também ganhou uma altura, relativa ao cateto perpendicular ao chão, marcado em verde:

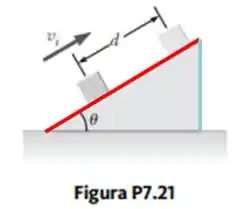
O nosso interesse é saber justamente o quanto ele subiu no cateto marcado em verde, que equivale a , a altura final do bloco em relação à Terra.

Uma relação que se estabelece entre o cateto verde, oposto ao ângulo e a hipotenusa, em vermelho, é a relação , que no caso vai ser .

Essa relação, matematicamente, é:

Como o bloco se locomoveu por na hipotenusa, vamos usar esse valor pra ela. A gente sabe que . Com isso, nossa incógnita vai ser a altura atingida no cateto verde, equivalente a .

Vamos ter:

Isolamos , tendo então:

Agora a gente já pode calcular que queríamos lá no começo do Passo 2.

Considerando

gente vai ter, por fim:

(c)Aqui, a gente começa verificando a diferença de energia da situação inicial (bloco com velocidade subindo a rampa) pra situação final (bloco parado, em uma posição mais alta).

A energia do bloco na situação inicial é apenas do tipo cinética, sendo:

A energia do bloco na situação final, em repouso, é só do tipo potencial gravitacional, que vai valer:

Repara, se no início o bloco tinha e no final apenas , é porque ao longo do percurso ele perdeu energia, na forma de atrito!

A gente pode escrever isso aqui:

E, com isso, temos:

Onde é a energia perdida em atrito. Pela formulinha, a gente tem:

A gente conhece e , e, assim, calculamos ! A gente vai ter:

(d)Pela formulinha pra força de atrito, a gente tem:

Onde é o coeficiente de atrito que a gente quer determinar e é a força normal.

Com isso, a gente precisa determinar pra podermos calcular . Olha só esse esqueminha:

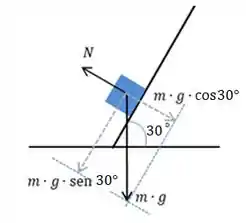
Pela decomposição dos vetores que representam as forças sobre o bloco, a gente conclui que a força normal precisa ser de igual módulo à decomposição perpendicular do vetor peso à rampa, já que o bloco não afunda na rampa e nem flutua sobre a mesma!

Com isso:

Assim:

Finalmente, a gente pode determinar o coeficiente de atrito . A gente vai ter: