Exercícios de Atrito e Forças não Conservativas - Lista de Exercícios Resolvida
Questão 1
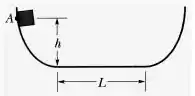
A figura mostra o perfil suave de uma calha com um trecho inclinado , seguido de um trecho horizontal , que é seguido de um outro trecho inclinado ; as alturas do ponto e do ponto acima do solo são iguais a e o comprimento do trecho horizontal é igual a . Um bloco de massa e dimensões desprezíveis desce a partir do ponto , onde o módulo da sua velocidade é e percorre os trechos , e . O coeficiente de atrito cinético entre o bloco e a calha no trecho é , e entre o bloco e a calha nos trechos e é zero. Considerando como dados , , e o módulo da aceleração da gravidade, calcule:
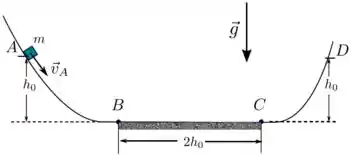
- Os trabalhos das forças peso e normal nos trechos , e ;
- O trabalho da força de atrito no trecho ;
- A variação da energia cinética do ponto ao ponto e o módulo da velocidade do bloco em ;
Questão 2
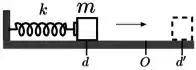
Um pequeno bloco de massa sobre uma mesa horizontal comprime uma mola de constante elástica de uma distância , a partir da posição relaxada da mola em , como mostra a figura. Liberado a partir do repouso, ele realiza um movimento retilíneo horizontal para a direita, onde ele perde o contato com a mola depois da posição , percorrendo em seguida uma distância , quando atinge o repouso; há uma força de atrito constante da supercifie da mesa sobre o bloco em toda a extensão do movimento. O coeficiente de atrito cinético entre a superfície e o bloco é:
Questão 3
Dois blocos idênticos de massa ligados por um fio ideal estão dispostos como mostra na figura abaixo. O bloco , se encontra sobre uma superfície horizontal cujo coeficiente de atrito cinético vale enquanto o bloco encontra-se pendurado. O sistema parte do repouso e ambos os blocos tem a mesma velocidade até o momento em que o bloco toca a mola. A constante elástica da mola é desconhecida. Determine:
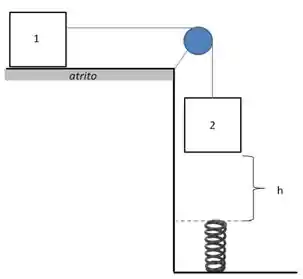
o trabalho realizado pela força de atrito no sistema quando o bloco cai uma altura . Este trabalho é positivo ou negativo? Justifique.
A velocidade do bloco ao tocar a mola.
Quando o bloco toca a mola, o fio entre os blocos é cortado instantaneamente. Observa-se que a velocidade do bloco neste instante é de . Sabendo que a compressão máxima que será produzida na mola é . Determine:
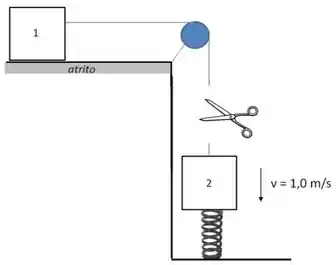
a constante elástica da mola em .
a que distância abaixo do ponto inicial de contato entre o bloco e a mola encontra-se o ponto de equilíbrio do sistema bloco e mola.
Ver solução completaQuestão 4
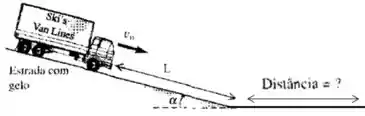
O freio de um caminhão de massa deixa de funcionar quando ele está descendo uma estrada de montanha com gelo inclinada de um ângulo . Inicialmente o caminhão desce a montanha com velocidade . Depois de percorrer, com atrito desprezível, uma distância até a base da montanha, o motorista vira o voltante e faz o caminhão seguir por uma estrada de emergência para caminhões. A estrada para caminhões é pavimentada com areia fofa que possui um atrito de rolamento igual a . Qual é à distância percorrida pelo caminhão desde a rampa até parar? Use o método da energia.
Questão 5
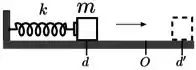
Um pequeno bloco de massa sobre uma mesa horizontal comprime uma mola de constante elástica de uma distância , a partir da posição relaxada da mola em , como mostra a figura. Liberado a partir do repouso, ele realiza um movimento retilíneo horizontal para a direita, onde ele perde o contato com a mola depois da posição , percorrendo em seguida uma distância , quando atinge o repouso; há uma força de atrito constante da supercifie da mesa sobre o bloco em toda a extensão do movimento. O coeficiente de atrito cinético entre a superfície e o bloco é:
Questão 6
Dois blocos e com massas de e estão ligados através de uma corda e de uma polia sem atrito de massas desprezíveis. Veja o desenho ao lado. A distância entre os pontos e indicados na figura é de . Existe atrito entre o bloco e o plano inclinado e o coeficiente de atrito cinético é igual a . Os blocos são soltos a partir do repouso.
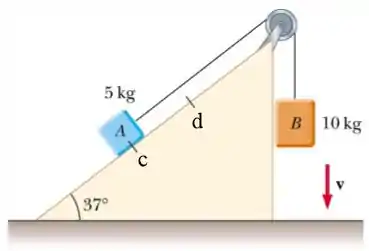
a) Calcule o trabalho realizado pela força da gravidade nos blocos e quando o bloco percorre a distância entre os pontos e .
b) Calcule a variação das energias cinética e potencial do sistema quando o bloco percorre a distância entre os pontos e .
c) Suponha agora que a partir de uma outra condição inicial o bloco chegue ao ponto com uma velocidade de e que neste instante o bloco tenha sua energia mecânica totalmente dissipada na colisão com o solo. Calcule a distância percorrida até que o bloco pare.
d) Finalmente suponha que no trecho entre os pontos e o atrito variasse linearmente com a distância percorrida, de tal forma que em a força de atrito fosse nula e em a força de atrito fosse igual a . Calcule o trabalho realizado pelo atrito sobre o corpo nestas condições.
Ver solução completaQuestão 7
Um objeto efetua um deslocamento sujeito à ação de duas forças, uma força conservativa e uma força dissipativa . Seja o trabalho realizado pela força conservativa e o trabalho realizado pela força dissipativa.
Sobre a variação da energia do objeto durante o deslocamento, é INCORRETO afirmar que:
(A) A variação da energia cinética do objeto é .
(B) A variação da energia potencial do objeto é
(C) A variação da energia térmica do objeto é
(D) A variação da energia mecânica do objeto é
(E) A energia total do objeto não é conservada durante o deslocamento.
Ver solução completaQuestão 8
Um grande bloco de massa deve ser transportado horizontalmente através de uma distância total de sobre um piso com atrito. Um trator empurra o bloco durante os primeiros com uma força variável, descrita pelo gráfico abaixo.
Tome .
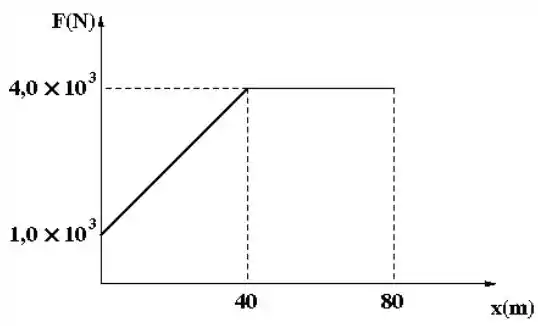
a) Calcule o trabalho total realizado pelo trator sobre o bloco.
b) Sabendo que o bloco chega totalmente em repouso ao fim dos , encontre o coeficiente de atrito cinético entre o bloco e o piso.
c) Ache a velocidade do bloco na posição .
Ver solução completaQuestão 9
Um caminhão reboque com massa puxa, utilizando uma corrente, um carro com massa em uma ladeira com inclinação de 20° em relação à horizontal. Devido ao tipo de reboque, tanto a corrente quanto o carro ficam inclinados em relação à ladeira de 30°. As forças de atrito que atuam entre a ladeira e os pneus do carro e do reboque são respectivamente e . O reboque e o carro partem do repouso e sobem a ladeira com aceleração constante. A tensão na corrente é igual a . Após subirem , reboque e carro estão a uma velocidade . Use
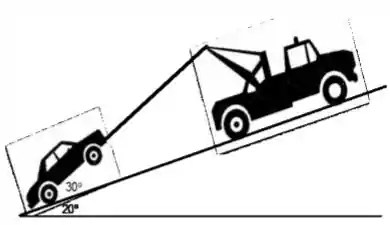
a) Calcule o trabalho feito pela corrente sobre o carro após puxa-lo por ladeira acima.
b) Calcule os trabalhos da força gravitacional sobre o carro e sobre o reboque nesta mesma distância.
c) Calcule os trabalhos do atrito sobre o carro e sobre o reboque nesta mesma distância.
d) Calcule o trabalho realizado pelo motor do reboque sobre o conjunto nesta mesma distância.
Ver solução completaQuestão 10
Em um bate-estaca, o martelo com massa é elevado até uma altura acima do topo de uma viga vertical que deve ser cravada no solo. Cada vez que o martelo é solto e colide com a viga e ela desce para dentro do solo. O martelo é guiado por trilhos verticais que produzem nele uma força de atrito constante de módulo igual a . Utilize considerações de trabalho e energia para responder as perguntas abaixo.
a) Calcule os trabalhos realizados pela força da gravidade e pela força de atrito sobre o martelo, desde quando ele é solto até o instante em que ele atinge a viga. Considere o eixo positivo apontando para cima.
b) Calcule o módulo da velocidade com que o martelo atinge a viga.
c) Considere que a colisão entre o martelo e a viga é completamente inelástica e que a massa da viga é igual a . Calcule a força média resultante que age sobre o sistema martelo-viga enquanto a viga está sendo cravada.
d) Calcule o percentual de energia dissipada em relação à energia inicial durante a colisão.
Ver solução completaQuestão 11
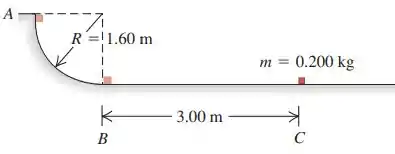
Em um posto de carga de caminhões do correio um pacote de é largado do repouso no ponto sobre um trilho com forma de um quarto de circunferência de raio igual a (veja a figura). O tamanho do pacote é muito menor do que , de modo que ele pode ser considerado como uma partícula. Ele desliza para baixo ao longo do trilho e atinge o ponto com uma velocidade de . Depois de passar pelo ponto , ele desliza uma distância de sobre uma superfície horizontal até parar no ponto .
(a) Qual é o coeficiente de atrito cinético entre o pacote e a superfície horizontal?
(b) Qual é o trabalho realizado pela força de atrito ao longo do arco circular do ponto A ao ponto B?
Questão 12
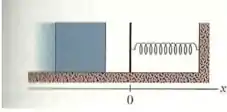
5) Considere a figura ao lado. O bloco de massa tem uma velocidade inicial e comprime a mola de constante elástica por uma distância até parar. (b) calcule considerando um coeficiente de atrito cinético de e .
Questão 14
Um bloco de massa m desce de uma distância d ao longo de uma superfície plana inclinada, fixa ao solo, que faz um ângulo θ com a horizontal. O coeficiente de atrito cinético entre o bloco e a superfície vale µc. Os trabalhos realizados pelas forças gravitacional, normal e força de atrito valem, respectivamente:
(a) +mgd sen θ, 0, −µcmgd cos θ
(b) +mgd cos θ, 0, −µcmg dsen θ
(c) +mgd sen θ, 0, +µcmgd cos θ
(d) −mgd sen θ, −mgd sen θ, −µcmgd cos θ
(e) −mgd sen θ, −mgd, +µcmgd cos θ
(f) +mgd sen θ, mgd, −µcmgd sen θ
Ver solução completaQuestão 15
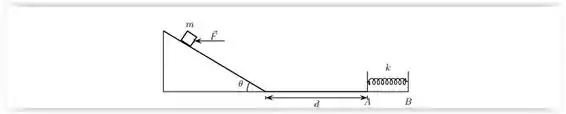
Um bloco de massa m desce acelerado ao longo de uma rampa inclinada de um angulo em relação à horizontal, como indicado na figura. Um dispositivo exerce sobre o bloco uma força constante horizontal, como indicado na figura. O coeficiente de atrito cinético entre a superfície do plano inclinado e o bloco vale µ. Ao atingir a base do plano inclinado, o bloco tem uma velocidade e o dispositivo que exerce a força é desligado. O bloco percorrerá uma distância sobre uma superfície horizontal, com o mesmo coeficiente de atrito µ até encontrar a extremidade de uma mola de constante elástica k, fixa na outra extremidade. Considere desprezível o atrito na região A-B. (Todas as respostas devem ser dadas em termos de m, , F, µ, g, k, v0 e d)
- represente e identifique todas as forças que agem sobre o bloco enquanto ele esta sobre o plano inclinado;
- determine o modulo da aceleração com que o bloco desce o plano;
- calcule a compressao máxima da mola.
Questão 16
Um bloco de massa está preso a uma mola de constante elástica . O coeficiente de atrito cinético entre o bloco e a mesa é . O bloco é puxado de uma distância da posição de equilíbrio, é solto a partir do repouso e para exatamente na posição . O coeficiente de atrito cinético é
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 17
Dois objetos A e B de massas M e 2 M , respectivamente, são deslocados de uma distância d ao longo de um plano inclinado por uma força F paralela ao plano . O coeficiente de atrito cinético entre as superfícies de cada objeto e a do plano inclinado tem o mesmo valor c. No ponto mais alto, pode-se afirmar que
(A)
(B)
(C)
(D) O trabalho realizado por sobre o corpo A é maior do que o trabalho realizado por sobre o corpo B.
E) O trabalho realizado por sobre o corpo A é menor do que o trabalho realizado por sobre o corpo B.
Ver solução completaQuestão 18
Um bloco de massa é solto em repouso do alto de um plano inclinado de ângulo em relação ao plano horizontal, com coeficiente de atrito cinético . Depois de percorrer uma distância ao longo do plano, o bloco colide com uma mola de constante elástica , de massa desprezível, que se encontrava relaxada.
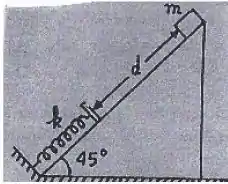
- Marque as forças atuantes sobre o bloco no momento da compressão. Calcule o trabalho realizado por cada uma das forças atuantes no problema desde o alto do plano até compressão máxima sofrida pela mola. Ache também o trabalho realizado pela força resultante.
- Ache a compressão sofrida pela mola para , , , e .
- Qual é a energia dissipada pelo atrito durante o trajeto máximo do bloco desde o alto do plano até compressão máxima sofrida pela mola?
- Após a compressão, a partícula retorna à sua posição de equilíbrio e liberta-se da mola, subindo ao longo do plano inclinado. Até que altura ela sobe?
Questão 19
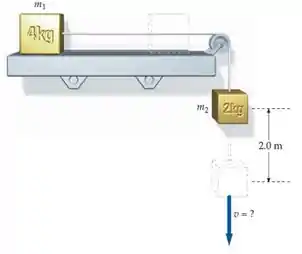
(Cap 7 – Ex 67) Na figura abaixo, o coeficiente de atrito cinético entre o bloco de e a prateleira é . (a) Encontre a energia dissipada por atrito quando o bloco de cai por uma distância . (b) Encontre a variação na energia mecânica do sistema dois-blocos-Terra durante o tempo que o bloco de leva para cair pela distância . (c) Use seu resultado da parte (b) para encontrar a rapidez de um dos blocos depois que o bloco de cai por .
Questão 20
Um vagão de carga com se desloca ao longo de trilhos horizontais com atrito desprezível e velocidade constante. O vagão é parado por uma combinação de duas molas em espiral, como ilustra a figura. As duas molas obedecem à lei de Hooke e suas constantes elásticas valem e . Após a primeira mola ser comprimida por uma distância , a segunda mola passa a agir juntamente com a primeira para aumentar a intensidade da força aplicada ao vagão. A força do conjunto é mostrada no gráfico abaixo. O vagão é parado a uma distância após o contato com a primeira mola. Todas as respostas devem ser fornecidas utilizando APENAS considerações sobre o trabalho realizado por uma força e o teorema do trabalho – energia cinética. Todos os cálculos devem ser justificados.
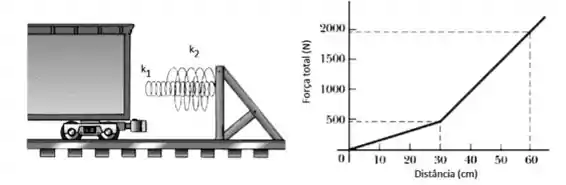
(a) Calcule qual é o trabalho realizado por cada uma das forças que atua sobre o vagão durante sua frenagem.
(b) Calcule qual é o módulo da velocidade do vagão logo antes dele encostar na primeira mola.
(c) Suponha agora que uma força de atrito atue entre os trilhos e o vagão e que o mesmo possua velocidade logo antes dele entrar em contato com a primeira mola. Se o vagão para a uma distância após o contato com a primeira mola, calcule o valor do coeficiente de atrito cinético entre os trilhos e o vagão.
Ver solução completaQuestão 21
Um bloco desliza de A para C ao longo de uma pista sem atrito e depois passa para um trecho horizontal CD com atrito. Qual das seguintes afirmações é verdadeira?
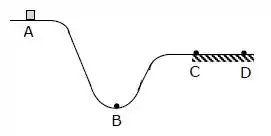
(A) No trecho AB a energia mecânica do bloco aumenta.
(B) Quanto maior a massa do bloco maior a distância que ele percorre no trecho CD até parar.
(C) No trecho CD a energia mecânica do bloco diminui.
(D) Nos trechos AB e BC a energia cinética do bloco aumenta.
(E) Nos trechos AB e BC a energia potencial gravitacional do bloco diminui.
Ver solução completaQuestão 22
Um disco de plástico de 75 g é arremessado de um ponto 1,1 m acima do solo, com uma velocidade escalar de 12 m/s. Quando o disco atinge uma altura de 2, 1 m, sua velocidade é 10,5 m/s. Qual é a redução da Emec do sistema disco-Terra devido ao arrasto do ar?
Ver solução completaQuestão 23
A figura mostra o perfil suave de uma calha com um trecho inclinado , seguido de um trecho horizontal , que é seguido de um outro trecho inclinado ; as alturas do ponto e do ponto acima do solo são iguais a e o comprimento do trecho horizontal é igual a . Um bloco de massa e dimensões desprezíveis desce a partir do ponto , onde o módulo da sua velocidade é e percorre os trechos , e . O coeficiente de atrito cinético entre o bloco e a calha no trecho é , e entre o bloco e a calha nos trechos e é zero. Considerando como dados , , e o módulo da aceleração da gravidade, calcule:
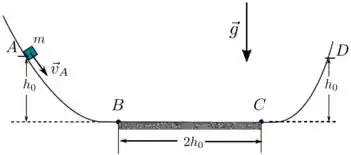
- Os trabalhos das forças peso e normal nos trechos , e ;
- O trabalho da força de atrito no trecho ;
- A variação da energia cinética do ponto ao ponto e o módulo da velocidade do bloco em ;
Questão 24
Um bloco de massa e dimensões desprezíveis encontra-se sobre um plano horizontal. Ele comprime uma mola de constante elástica no pondo de uma distância em relação à posição ; conforme mostra a figura. Liberado neste ponto a partir do repouso ele percorre o trajeto perdendo contato com a mola no ponto , onde a mola está relaxada. Somente entre e , separados de uma distância desconhecida há atrito. O coeficiente de atrito cinético entre as superfícies do bloco e do plano na região . Após o ponto há uma rampa sem atrito. A partir do ponto , final da rampa, a superfície é horizontal e tem uma altura em relação à horizontal do trecho ; vide a figura.
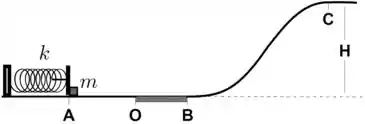
- Determine a velocidade do bloco no ponto ;
- Determine a distância entre os pontos e , dispondo que a velocidade do bloco em é nula;
- Determine a compressão mínima, , da mola necessária para que o bloco atinja o ponto no topo da rampa.
Questão 25
Um bloco de massa desliza por uma superfície como mostra a figura abaixo. A superfície tem atrito só na rampa que forma um ângulo com a horizontal; este atrito tem um coeficiente cinético Assuma que o bloco parte do repouso.

Parte
- Usando somente conceitos de energia, determine o valor da altura máxima em função dos dados conhecidos, isto é, (
- Supondo , , encontre a variação de energia potencial e a variação de energia cinética, quando a força desloca o corpo de para . Despreze qualquer atrito.
Parte Seja uma força conservativa, dada em Newtons, que atua sobre um corpo de onde e são duas constantes positivas e é dado em metros. Utiliza .
Questão 26
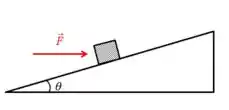
A ação de uma força de módulo aplicada na direção horizontal de um bloco de massa , faz com que ele suba uum plano inclinado de com a horizontal. O coeficiente de atrito cinético entre o bloco e o plano inclinado é Durante o trajeto, o bloco se desloca ao longo do plano uma distância O bloco parte da base do plano e do repouso. Utilize:
- Calcule o trabalho efetuado por cada uma das forças que atuam no bloco durante o trajeto de subida ao longo do plano inclinado. Justifique seus cálculos.
- Calcule a variação da energia cinética durante todo o percurso. Justifique seu cálculo
- Suponha uma outra situação, onde o mesmo bloco sobe o plano inclinado sob a ação de uma outra força de módulo aplicada na direção paralela ao plano inclinado. Existe atrito entre o bloco e o plano, mas neste caso, o módulo da força de atrito cinético varia com a velocidade do bloco e é dada em Newtons por , onde é dada em . Calcule o módulo da força e a potência fornecida por ela ao bloco quando a velocidade do bloco for igual a sabendo que a aceleração do bloco ao longo do plano no mesmo instante é dada por
Questão 27
Q - Uma mola, de constante elástica , é usada, em um parque de diversões, para lançar pessoas em um escorregador de altura , como mostra a figura abaixo. A pista do escorregador não tem atrito desde o início (ponto de lançamento das
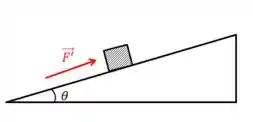
pessoas) até o ponto (começo da subida da rampa), onde o coeficiente de atrito passa a ser . A inclinação da rampa é tal que e . Se uma pessoa de massa for lançada quando a mola está comprimida em relação ao seu comprimento natural, a distância que ela percorrerá na rampa antes de parar, em metros, é:
• Considere a pessoa como uma partícula de massa .
Questão 28
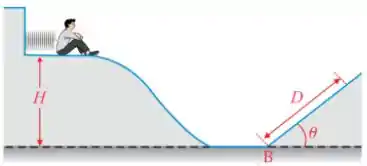
Q - Um bloco de massa é largado do ponto de uma altura , como mostra a figura abaixo. Ele percorre um caminho sem atrito até o ponto . Em seguida, ele atravessa uma região com atrito, apenas entre os pontos e , de comprimento , até colidir com uma mola de constante de força , comprimindo-a em , até parar. Podemos afirmar que o coeficiente de atrito existente na região entre os pontos e vale:
- Considere o bloco como uma partícula de massa .
Questão 29
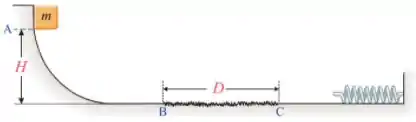
Uma corda é usada para puxar um bloco de massa com velocidade constante ao longo de uma superfície horizontal com atrito. A força constante que a corda exerce no bloco possui módulo e direção formando um ângulo com a horizontal (ver figura a seguir). O bloco se desloca horizontalmente.
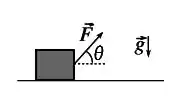
Calcule:
(a) o trabalho desta força ao longo de um deslocamento de comprimento do bloco;
(b) o coeficiente de atrito cinético entre o bloco e a superfície horizontal;
(c) o trabalho da força de atrito ao longo deste deslocamento . Se a força é conservativa, de quanto variou a sua energia potencial neste deslocamento?
Ver solução completaQuestão 30
Um bloco de massa desliza ao encontro de uma mola de constante elástica , sobre uma superfície horizontal. O bloco é parado após comprimir a mola de um comprimento . Ao longo de todo o percurso há atrito entre o bloco e o piso, sendo o coeficiente de atrito cinético . O quadrado da velocidade com que o bloco deve atingir a mola antes de ser comprimida é dado por
a)
b)
c)
d)
e)
Ver solução completaQuestão 31
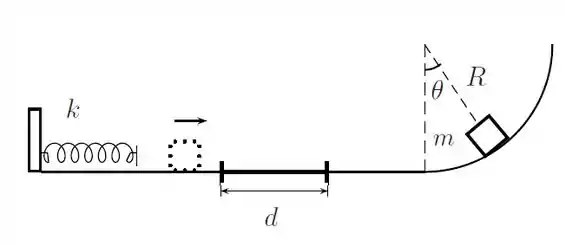
Um pequeno bloco de massa , após ser empurrado a partir do repouso por uma mola de constante elástica , comprimidade uma distância , desliza sobre uma superfície horizontal. Após se soltar da mola, ele passa por um trecho de comprimento , única região em que o atrito não é desprezível e cujo coeficiente de atrito cinético é . No final desta superfície horizontal, o bloco começa a subir uma rampa vertical semicircular de raio . Uma vez na rampa o bloco atinge uma posição, cuja direção faz um ângulo , desconhecido, com a vertical, onde para momentaneamente e volta descendo a rampa; como mostra a figura. Calcule
a) a velocidade do bloco imediatamente antes de começar a subir a rampa semicircular;
b) o ângulo alcançado;
c) o módulo da força normal, ao atingir o ângulo . Apresenta a resposta em função dos dados do problema e do ângulo ;
d) o módulo da velocidade máxima do bloco durante o seu movimento e onde ela ocorre; justifique sua resposta.
Questão 32
Questão 33
Dois blocos idênticos de massa ligados por um fio ideal estão dispostos como mostra na figura abaixo. O bloco , se encontra sobre uma superfície horizontal cujo coeficiente de atrito cinético vale enquanto o bloco encontra-se pendurado. O sistema parte do repouso e ambos os blocos tem a mesma velocidade até o momento em que o bloco toca a mola. A constante elástica da mola é desconhecida. Determine:
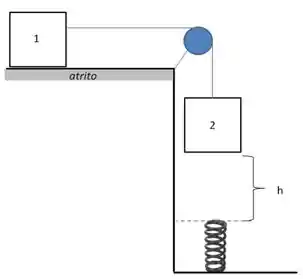
o trabalho realizado pela força de atrito no sistema quando o bloco cai uma altura . Este trabalho é positivo ou negativo? Justifique.
A velocidade do bloco ao tocar a mola.
Quando o bloco toca a mola, o fio entre os blocos é cortado instantaneamente. Observa-se que a velocidade do bloco neste instante é de . Sabendo que a compressão máxima que será produzida na mola é . Determine:
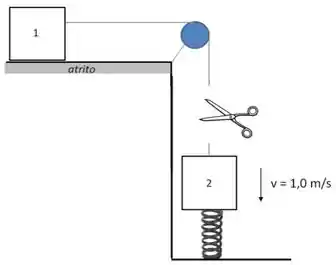
a constante elástica da mola em .
a que distância abaixo do ponto inicial de contato entre o bloco e a mola encontra-se o ponto de equilíbrio do sistema bloco e mola.
Ver solução completaQuestão 34
Dois pequenos discos, de massas e , se deslocam sobre uma mesa horizontal de coeficiente de atrito cinético com os discos . Inicialmente os discos possuem velocidades em direções perpendiculares cujos módulos são desconhecidos. Em um certo instante os discos colidem e passam a se deslocar juntos. Após a colisão o sistema se movimenta em uma direção que faz um ângulo com o eixo conforme a figura. Além disso observa-se que o sistema entra em repouso após percorrer uma distância d desde o ponto onde ocorreu a colisão. Desprezando efeitos de rotação de cada disco, determine:
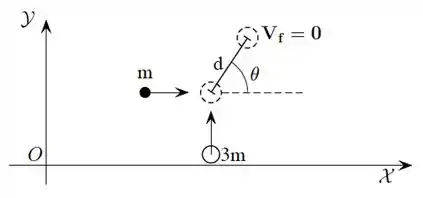
(a) O trabalho realizado pela força de atrito entre o instante da colisão e aquele em que os discos entram em repouso.
Ver solução completaQuestão 35
Um objeto move-se do ponto A ao ponto B sob a ação de apenas duas forças. Uma das forças é dissipativa e realiza um trabalho de ; a outra força é conservativa e realiza um trabalho de . Entre A e B
(A) A energia cinética do corpo aumenta e a energia mecânica diminui.
(B) A energia cinética do corpo diminui e a energia mecânica diminui.
(C) A energia cinética do corpo diminui e a energia mecânica aumenta.
(D) A energia cinética do corpo aumenta e a energia mecânica aumenta.
(E) Nenhuma das respostas anteriores.
Ver solução completaQuestão 36
Um bloco de massa , sobre um plano inclinado de ângulo está preso por uma corda que passa por uma polia e se conecta a uma mola de constante elástica , como mostra a figura abaixo.
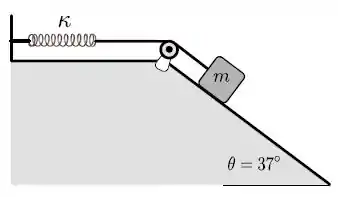
O bloco é liberado a partir do repouso quando a mola encontra-se relaxada em seu comprimento natural. Considere que as massas da corda e da polia, e o atrito no plano e na polia são desprezíveis. Dados:
; ; .
(a) Obtenha a velocidade do bloco após percorrer a distância .
(b) Calcule a maior distância que o bloco percorre sobre o plano antes de parar momentaneamente.
Considere agora que existe atrito entre o bloco e o plano com coeficiente de atrito cinético .
(c) Calcule qual será a nova distância que o bloco percorre sobre o plano antes de parar momentaneamente, neste caso.
Ver solução completaQuestão 37
Com relação a um carro de massa , descendo uma montanha russa de altura inicial , marque a alternativa incorreta:
(A) Se não houverem forças dissipativas, a energia mecânica se conserva.
(B) Se não houverem forças dissipativas, a variação de energia cinética final.
(C) Se houverem forças dissipativas, a energia interna do sistema aumenta durante o movimento.
(D) Se houverem forças dissipativas, a energia mecânica é igual ao negativo do trabalho da força peso atuando sobre o carro.
(E) Se houverem forças dissipativas, variação de energia cinética final.
Ver solução completaQuestão 38
Um bloco de massa está parado sobre uma superfície, preso a uma mola presa a uma parede, como mostrado na figura abaixo; A mola tem massa desprezível, constante de mola e comprimento quando não está comprimida. O coeficiente de atrito estático entre o bloco e o chão é . Espresse suas respostas em termos de , , , e constantes fundamentais.
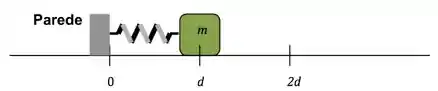
(c) O bloco é colocado na posição e solto, permanecendo em repouso. Quando o bloco é deslocado um pouco para a direita desta posição, o bloco começa a se mover sobre a superfície com um coeficiente de atrito cinético .
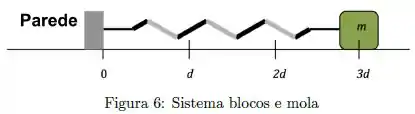
I. Em termos das variáveis dadas, qual o valor de ?
II. Quanta energia potencial está armazenada no sistema mola-massa logo antes do sistema começar a se mover?
III. O bloco desliza uma distância antes de parar novamente. Determine o coeficiente de atrito cinético .
IV. Em qual posição o bloco tem a velocidade máxima durante o período em que ele se move? DICA: Qual deve ser a aceleração do bloco neste ponto?
V. Qual a velocidade máxima do bloco durante este movimento?
Ver solução completaQuestão 39
Um elevador de massa está em repouso a uma altura de , medida a partir do fundo do poço, quando o seu cabo rompe. O dispositivo de segurança do elevador é ativado de forma instantânea, mas não funciona corretamente. O elevador então inicia um movimento de descida lenta deslizando sobre trilhos laterais os quais geram uma força de atrito intensa e constante igual a . No fundo do poço há uma mola de comprimento igual a (quando relaxada), que vai auxiliar o trilho a parar o elevador. A constante elástica da mola é desconhecida. Depois da mola ser comprimida de o elevador entra em repouso. Utilize para a aceleração da gravidade. Suponha a origem do potencial como sendo o fundo do poço.
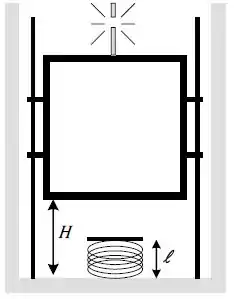
a) Determine a energia cinética do elevador na iminência de encostar na mola, em função dos dados do problema.
b) Assumindo que a energia cinética do elevador na iminência de encostar na mola é , determine a energia máxima armazenada na mola, em função dos dados do problema.
c) Utilize somente para este item os seguintes dados numéricos: , , , , 𝑒 . Calcule a energia potencial gravitacional do elevador quando ele estiver em repouso na posição do item b).
Ver solução completaQuestão 40
Na figura temos um pequeno bloco de massa em quilogramas, que parte do ponto A numa superfície horizontal com velocidade . O percurso é sem atrito até o trecho de comprimento , em que o coeficiente de atrito cinético é . As alturas indicadas são e . Considere a origem do potencial como sendo no ponto A.
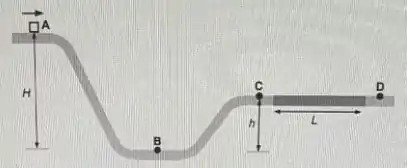
(a) Determine as energias potencial e cinética do bloco no ponto B (responda em função da massa do bloco).
(b) Determine a velocidade do bloco no ponto C.
(c) O bloco atinge o ponto D? Caso a resposta seja afirmativa, determine a velocidade do bloco nesse ponto; caso a resposta seja negativa. Calcule a distância que o bloco percorre na parte com atrito.
Ver solução completaQuestão 41
Na figura abaixo estão indicadas 3 posições identificadas pelas letras , e . Um Bloco de massa inicialmente em repouso a uma altura a partir do solo está em contato com uma mola comprimida. A mola possui constante elástica .
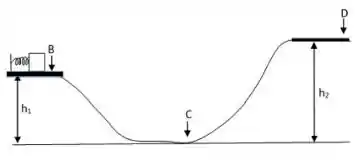
Após a mola ser solta e o bloco se desprender, o bloco desliza sem atrito passando pelo ponto que se encontra na mesma altura . Segue descendo por uma rampa até o ponto . Neste ponto o bloco possui velocidade . Após passar o ponto , o bloco volta a subir por uma segunda rampa de altura até uma plataforma horizontal. Esta plataforma possui atrito e o bloco desliza até parar no ponto . O coeficiente de atrito cinético na plataforma vale .
Use para a aceleração da gravidade. As variáveis dadas do problema são (, , , , e )
a) Determine a compressão da mola em termos das variáveis dadas do problema.
b) Determine a velocidade do bloco no ponto em termos das variáveis do problema.
c) Determine a distância percorrida na plataforma em termos das variáveis dadas.
d) Calcule a menor altura de modo que acima dela o bloco volta a tocar na mola.
Ver solução completaQuestão 42
Um bloco de madeira de massa está inicialmente em repouso sobre uma superfície horizontal de atrito desprezível. Uma mola ideal tem uma de suas extremidades ligada ao bloco enquanto a outra extremidade está ligada a uma parede. Inicialmente a mola não está distendida nem comprimida. Uma bala de massa , com velocidade horizontal de módulo , atinge o bloco e nele fica alojada, fazendo com que a mola seja comprimida de uma distância .
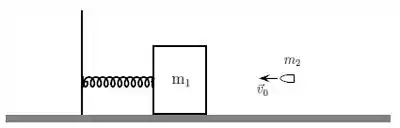
a) Qual o módulo da velocidade do bloco imediatamente após ser atingido pela bala?
b) Qual a constante elástica da mola?
c) Supondo agora que exista atrito entre o bloco e o chão com um coeficiente de atrito cinético entre as superfícies . Calcule qual deve ser a constante elástica de uma outra mola que substituiu a primeira para que a compressão máxima da mola continue sendo .
Ver solução completaQuestão 43
Considere uma esteira muito longa que se move com uma velocidade constante de (um motor mantém essa velocidade). Jogamos sobre essa esteira caixas de a uma taxa de caixa por segundo. Cada caixa inicialmente escorrega sobre a esteira, mas devido ao atrito cinético, cujo coeficiente é , as caixas terminam por se mover com a mesma velocidade da esteira. Considere que as caixas caem verticalmente sobre a esteira.
Qual o valor da energia cinética fornecida para cada caixa?
Qual o módulo da força de atrito?
Que energia é fornecida pelo motor ao sistema, para cada caixa que cai?
Conforme as caixas vão caindo sobre a esteira, qual deve ser a força que o motor deve exercer sobre a esteira de maneira a mantê-la a uma velocidade constante?
Ver solução completaQuestão 45
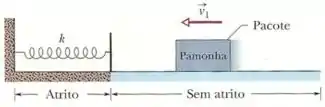
7) Um pacote com de pamonha, depois de deslizar ao longo de um piso com velocidade , choca-se com uma mola, comprimindo-a até ficar momentamente em repouso. Até o ponto em que o pacote entra em contato com a mola inicialmente relaxada o piso não possui atrito, mas enquanto o pacote está comprimindo a mola o piso exerce sobre o pacote uma força de atrito cinético de módulo . Se , qual é a variação do comprimento da mola entre o instante em que começa a ser comprimida e o instante em que o pacote para?
Questão 46
Questão 3). Na figura ao lado, o bloco , de massa , encontra-se inicialmente em repouso a uma altura , em uma pista sem atrito. O bloco é liberado e colide com o bloco , de massa , que estava inicialmente em repouso. Após a colisão, os blocos permanecem unidos e deslizam sobre a região com atrito e param depois de percorrerem uma distância . Sabendo que , determine o coeficiente de atrito cinético entre os blocos e o trecho com atrito. Os blocos são feitos do mesmo material. (Lembre-se que o coeficiente de atrito é uma grandeza adimensional)
Questão 47
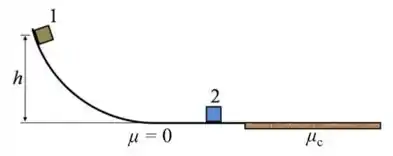
Uma caixa desliza sobre uma superfície horizontal com velocidade escalar de quando, no ponto , encontra uma área áspera. Na área áspera, o coeficiente de atrito não é constante, mas se inicia a em e aumenta linearmente conforme ultrapassa , atingindo um valor de a após o ponto .
c) Qual a distância a caixa percorreria, caso o coeficiente de atrito não aumentasse, mas, em vez disso, tivesse o valor constante de 0.100?
Ver solução completaQuestão 48
4) Um bloco de massa é solto, a partir do repouso, em um plano inclinado de em relação à horizontal, com coeficiente de atrito cinético . Depois de percorrer uma distância ao longo do plano inclinado, o bloco colide com uma mola de constante , de massa desprezível, que se encontrava inicialmente relaxada, de acordo com o esquema mostrado na figura ao lado.
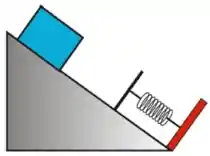
d) Se o coeficiente de atrito estático com o plano é de , o bloco continua parado ou começa a subir o plano inclinado depois de parar completamente?
Ver solução completaQuestão 49
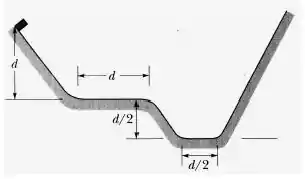
Um bloco é liberado a partir do repouso conforme a figura abaixo, iniciando seu movimento a partir da extremidade esquerda da figura. Os trechos em rampa não possuem atrito, e os trechos planos possuem atrito, com coeficiente de atrito cinético de . O valor de .
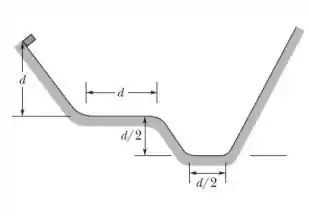
Durante seu movimento para a direita, qual a velocidade no final do primeiro trecho plano (mais alto)? Qual a velocidade no final do segundo trecho plano (mais baixo)? Qual a velocidade no final do segundo trecho plano (mais baixo)? Qual a altura máxima (em relação ao trecho plano mais baixo) que o bloco atinge na rampa da direita?
Ver solução completaQuestão 50
Um corpo de massa ao ser largado de uma altura , apartir do repouso, num plano inclinado de um ângulo em relação a horizontal, atinge uma velocidade de módulo ao chegar na base do plano. Há atrito entre o corpo e a superfície do plano sendo o coeficiente de atrito cinético igual a . O mesmo corpo quando largado sob as mesmas condições em outro plano de mesma inclinação, mas sem atrito, atinge a base do plano com uma velocidade cujo módulo é o dobro da situação anterior. O valor de é igual a:
Questão 51
Um bloco de massa é solto, a partir do repouso, em um plano inclinado de em relação à horizontal, com coeficiente de atrito cinético . Depois de percorrer uma distância de ao longo do plano inclinado, o bloco colide com uma mola de constante , de massa desprezível, que se encontrava inicialmente relaxada, de acordo com o esquema mostrado na figura ao lado.
a) Qual é a compressão sofrida pela mola?
Questão 52
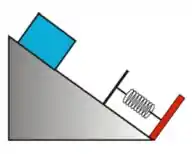
4) Um bloco de massa é solto, a partir do repouso, em um plano inclinado de em relação à horizontal, com coeficiente de atrito cinético . Depois de percorrer uma distância ao longo do plano inclinado, o bloco colide com uma mola de constante , de massa desprezível, que se encontrava inicialmente relaxada, de acordo com o esquema mostrado na figura ao lado.
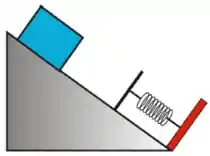
c) Qual a velocidade do bloco no momento em que entra em contato com a mola?
Ver solução completaQuestão 53
Um bloco é liberado a partir do repouso conforme a figura abaixo, iniciando seu movimento a partir da extremidade esquerda da figura. Os trechos em rampa não possuem atrito, e os trechos planos possuem atrito, com coeficiente de atrito cinético de . O valor de .
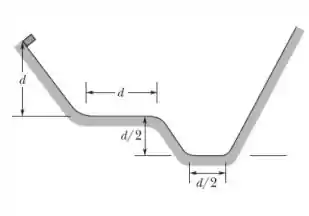
Após atingir essa altura máxima na rampa da direita, o bloco inicia o movimento contrário, se movendo agora da direita para a esquerda. Com que velocidade o bloco atinge o final do primeiro trecho plano (mais baixo)? Com que velocidade o bloco atinge o início do segundo trecho plano (mais alto)? Qual a posição exata em que o bloco para totalmente?
Ver solução completaQuestão 54
Duas caixas de massas e deslizam para baixo em um plano inclinado com com a horizontal. As caixas são ligadas por uma haste rígida sem massa paralela ao plano, conforme a figura ao lado. O coeficiente de atrito cinético entre a caixa e o plano é ; e entre a caixa e o plano é .
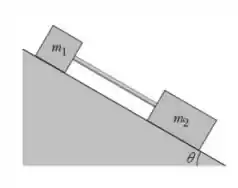
Qual a tração na haste?
Qual a aceleração das massas?
Se as posições das caixas fossem invertidas, o que mudaria nas respostas anteriores? Explique fisicamente a diferença.
Ver solução completaQuestão 55
Considere um plano inclinado que forma um ângulo de o com a horizontal. Na parte inferior do plano inclinado está uma mola com constante elástica de fixada num muro. Um bloco de inércia solto na parte superior do plano inclinado produz uma compressão máxima na mola de em relação à posição inicial

a) Desprezando todos os atritos calcule a distância que o bloco percorre desde o momento em que é solto até comprimir a mola no seu valor máximo.
b) Agora considere que existe atrito entre a superfície do bloco e o plano inclinado com . Calcule a distância em que o bloco foi solto para comprimir a mola do mesmo valor máximo anterior.
c) Qual a aceleração do bloco ao descer a rampa com atrito?
d) Se você quiser que o bloco desça com velocidade constante a rampa com atrito qual o ângulo a rampa dever ter com a horizontal
Ver solução completaQuestão 56
Uma ou duas forças agem sobre um disco metálico que se move sobre o gelo sem atrito ao longo do eixo , em movimento unidimensional. A massa do disco é . As forças , para direita, e , para esquerda, atuam ao longo do eixo e tem módulos e . Uma força faz um ângulo de com o eixo e tem módulo . Qual é a aceleração do disco quando apenas a força atua? Quando as forças e agem? E com todas as forças atuando sobre o disco?
Ver solução completaQuestão 57
Um bloco de massa está localizado no final de uma mola de constante elástica comprimida de . Após um certo instante, esta mola é solta e dispara o bloco, fazendo com que ele adquira velocidade e suba uma pequena rampa de altura . Ao final desta rampa, o bloco encontra um piso cujo o coeficiente de atrito entre o bloco e o piso vale . Todas as superfícies antes de atingir o piso do final da rampa possuem coeficiente de atrito desprezível. Dado: use para a gravidade.

c) Em função de , , , e determine a distância máxima que o bloco pode percorrer no trecho com atrito até parar.
Ver solução completaQuestão 58
Um bloco de massa inicialmente em repouso desliza para baixo em um plano inclinado que faz um ângulo com a horizontal. Depois de ter deslizado uma distância , o bloco colide com uma mola de constante elástica desconhecida. A mola reduz a velocidade do bloco até fazê-lo parar momentaneamente. Neste instante a mola está comprimida de uma distância . Não existe atrito entre o plano e o bloco até o contato com a mola (deslocamento ). Mas existe atrito entre plano e o bloco na região da mola (deslocamento ) com coeficiente de atrito cinético . Use para a aceleração da gravidade. Responda em função dos dados fornecidos utilizando a Lei de Conservação de Energia.
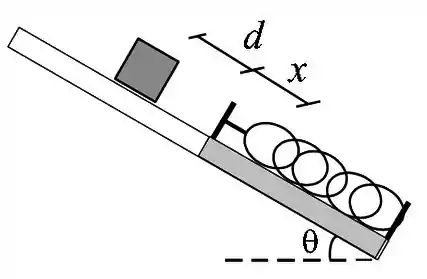
(b) Determine a energia potencial elástica armazenada na mola após ela ter sido totalmente comprimida, em função das variáveis dadas.
Ver solução completaQuestão 61
Uma pessoa com massa de sentada sobre uma prancha desce uma duna, que pode ser aproximada por uma rampa. A pessoa começa em repouso a uma altura de acima do nível da lagoa e desliza sobre a areia por uma distância duna abaixo, até atingir o nível da lagoa com velocidade de . A força de atrito cinético entre a prancha e a duna é . Qual é a distância percorrida pela pessoa no trajeto? Despreze a resistência do ar e considere .

Escolha uma:
Nenhuma das outras alternativas está correta.
Ver solução completaQuestão 62
Na Fig. 8-51, um bloco de massa desliza de encontro a uma mola de constante elástica . O bloco para após comprimir a mola . O coeficiente de atrito cinético entre o bloco e o piso é. Enquanto o bloco está em contato com a mola e sendo levado ao repouso, determine (a) o trabalho realizado pela mola e (b) o aumento da energia térmica do sistema bloco-piso. (c) Qual é a velocidade do bloco imediatamente antes de se chocar com a mola?
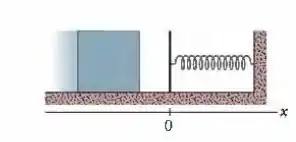
Figura 8-51 Problema 55.
Ver solução completaQuestão 63
(Cap 7 – Ex 65) O bloco de na figura desce por uma rampa curvada sem atrito, partindo do repouso a uma altura de . O bloco então desliza por sobre uma superfície horizontal rugosa até atingir o repouso. (a) Qual é a rapidez do bloco na base da rampa? (b) Qual é a energia dissipada por atrito? (c) Qual é o coeficiente de atrito cinético entre o bloco e a superfície horizontal?
Ver solução completaQuestão 64
Um objeto de 20,0 g de massa é posicionado contra a extremidade livre de uma mola de constante elástica igual a 25,0 N/m que é comprimida de 10,0 cm. Uma vez liberado, o objeto desliza 1,20 m, sobre a mesa, e cai no chão a 1,40 m da borda da mesa, como esquematizado na figura. A distância de deslizamento na mesa inclui os 10,0 cm de compressão da mola e a superfície da mesa está a 1,20 m acima do nível do solo. (Use g = 10,0 m/.)
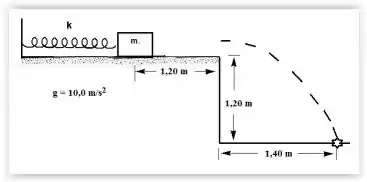
(a) Calcule a rapidez do objeto no instante em que perde contato com a borda da mesa.
(b) Mostre que existe atrito entre o objeto e a superfície da mesa.
(c) Calcule o coeficiente de atrito cinético.
Ver solução completaQuestão 65
10) Ao empurrar uma caixa com massa sobre um piso plano com velocidade constante, uma pessoa realiza trabalho a uma taxa . Se a rapidez da caixa é , qual o coeficiente de atrito cinético entre o piso e a caixa? Suponha que a força do empurrão da pessoa sobre a caixa seja exercida horizontalmente.
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 66
(Cap. 8 – Ex. 56) Um pacote de começa a subir um plano inclinado de com uma energia cinética de . Que distância ele percorre antes de parar, se o coeficiente de atrito cinético entre o pacote e o plano é ?
Ver solução completaQuestão 67
Uma partícula pode deslizar em uma pista com extremidades elevadas e uma parte central plana, como mostra a Fig. 8-56. A parte plana tem um comprimento . Os trechos curvos da pista não possuem atrito, mas na parte plana o coeficiente de atrito cinético é . A partícula é liberada a partir do repouso no ponto , que está a uma altura . A que distância da extremidade esquerda da parte plana a partícula finalmente para?
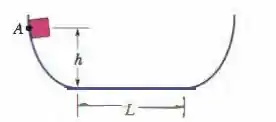
Figura 8-56 Problema 65.
Ver solução completaQuestão 68
O cabo do elevador de da Fig. 8-54 se rompe quando o elevador está parado no primeiro andar, onde o piso se encontra a uma distância acima de uma mola de constante elástica . Um dispositivo de segurança prende o elevador aos trilhos laterais, de modo que uma força de atrito constante de passa a se opor ao movimento. (a) Determine a velocidade do elevador no momento em que se choca com a mola. (b) Determine a máxima redução do comprimento da mola (a força de atrito continua a agir enquanto a mola está sendo comprimida). (c) Determine a distância que o elevador sobe de volta no poço. (d ) Usando a lei de conservação da energia, determine a distância total aproximada que o elevador percorre antes de parar. (Suponha que a força de atrito sobre o elevador seja desprezível quando o elevador está parado.)
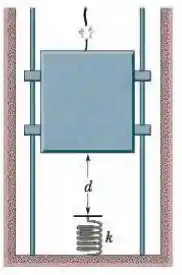
Figura 8-54 Problema 63.
Ver solução completaQuestão 69
Na Fig. 8 - 52, um bloco desliza ao longo de uma pista, de um nível para outro mais elevado, passando por um vale intermediário. A pista não possui atrito até o bloco atingir o nível mais alto, onde uma força de atrito para o bloco depois que ele percorre uma distância . A velocidade inicial do bloco é a diferença de altura é e é . Determine o valor de.
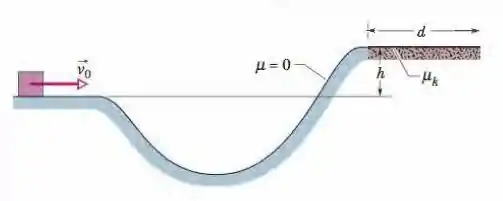
Figura 8-52 Problema 57.
Ver solução completaQuestão 70
Na Fig. 8-50, um bloco de é acelerado a partir do repouso por uma mola comprimida de constante elástica . O bloco deixa a mola no seu comprimento relaxado e se desloca em um piso horizontal com um coeficiente de atrito cinético . A força de atrito para o bloco em uma distância . Determine (a) o aumento de energia térmica do sistema bloco-piso, (b) a energia cinética máxima do bloco e ( c) o comprimento da mola quando estava comprimida.
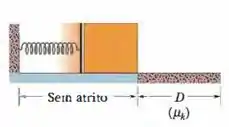
Figura 8-50 Problema 53.
Ver solução completaQuestão 71
Quando um besouro salta-martim está deitado de costas, pode pular encurvando bruscamente o corpo, o que converte a energia armazenada em um músculo em energia mecânica, produzindo um estalo audível. O videoteipe de um desses pulos mostra que um besouro de massa se desloca na vertical durante um salto e consegue atingir uma altura máxima . Qual é o valor médio, durante o salto, (a) do módulo da força externa exercida pelo piso sobre as costas do besouro e (b) do módulo da aceleração do besouro em unidades de g?
Ver solução completaQuestão 72
Um collie arrasta a caixa de dormir em um piso, aplicando uma força horizontal de . O módulo da força de atrito cinético que age sobre a caixa é. Quando a caixa é arrastada por uma distância de , quais são (a) o trabalho realizado pela força do cão e (b) o aumento de energia térmica da caixa e do piso?
Ver solução completaQuestão 73
Um operário empurra um caixote de , com velocidade constante, por , ao longo de um piso plano, com uma força orientada abaixo da horizontal. Se o coeficiente de atrito cinético entre o bloco e o piso é , quais são (a) o trabalho realizado pelo operário e (b) o aumento da energia térmica do sistema bloco-piso?
Ver solução completaQuestão 74
(Cap. 8 – Ex. 47) Um urso de escorrega, a partir do repouso, para baixo em um tronco de pinheiro, movendo-se com uma velocidade de imediatamente antes de chegar ao chão. (a) Qual é a variação da energia potencial gravitacional do sistema urso-Terra durante o deslizamento? (b) Qual é a energia cinética do urso imediatamente antes de chegar ao chão? (c) Qual é a força de atrito média que age sobre o urso enquanto está escorregando?
Ver solução completaQuestão 75
. Um bloco de massa é solto do repouso de uma altura (posição ) na pista ilustrada na figura. A pista é sem atrito, a menos de um trecho de comprimento e coeficiente de atrito cinético . O bloco chega à mola de constante elástica e a comprime até chegar a um repouso momentâneo. Determine a compressão máxima da mola, a velocidade do bloco em , quando este passa pelo trajeto pela segunda vez, a posição que o bloco para finalmente. Adote

Questão 76
. O sistema de transporte de passageiros sobre trilhos entre a base e o topo de uma montanha, mostrado na figura, é composto de um vagão (massa ), uma mola que obedece a lei de Hooke , polia e cabo ideais, e um contrapeso (massa ). O coeficiente de atrito cinético entre o vagão e os trilhos na montanha é . O ângulo entre a montanha e a horizontal é . O vagão, travado na base da montanha, recebe passageiros de massa . Em seguida, a trava é retirada, o vagão sobe a montanha e, ao atingir o topo, comprime a mola até parar. A distância total percorrida desde a retirada da trava até a compressão total da mola é de . Determine qual é a velocidade do vagão após percorrer os primeiros e a distância percorrida pelo vagão desde o instante em que toca a mola até parar.

Questão 77
Um carrinho de montanha russa se move sem atrito no trilho da figura abaixo. Ele sai do repouso do ponto A, situado a 40 metros do chão. Por questões de segurança, a força exercida no carrinho pelo trilho no ponto B não pode ser maior que 5 vezes o peso do carrinho.
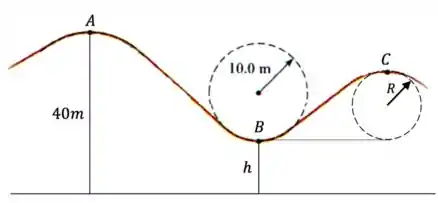
a) Considerando que no ponto A o carrinho descreve um círculo de raio 10 metros, qual deve ser a altura mínima ℎ para satisfazer o critério de segurança? Qual para essa altura mínima?
b) Considerando a altura mínima ℎ do item anterior, qual deve ser o raio mínimo R da curvatura no ponto C, que está a uma altura 2R acima de B, para que o carrinho não perca contato com o trilho quando passar por C? Qual para esse raio mínimo?
Ver solução completaQuestão 79
Uma caixa de massa igual a desliza por um plano com inclinação de A aceleração da caixa é de e o plano inclinado tem de comprimento.
(a) Qual é a energia cinética da caixa quando ela atinge a base do plano inclinado?
(b) Quanto trabalho é gasto para superar o atrito?
(c) Qual é a magnitude da força de atrito que atua na caixa conforme ela desliza pelo plano inclinado?
Ver solução completaQuestão 80
Um bloco de está sobre uma rampa com atrito e é conectado a um bloco de por uma corda ideal que passa por uma polia leve e sem atrito. O bloco de está ligado a uma mola que tem massa desprezível e uma constante de força de , como mostrado na figura. (O bloco de sempre está ligado a mola, ou seja, quando o bloco sobe a mola estica e se contrai quando o bloco desce).
A mola inicialmente está relaxada quando o sistema está na posição (a) mostrado na figura. O bloco de é puxado para baixo sobre a rampa (posição b) e então liberado a partir do repouso. (Ao ser liberado, o bloco da posição b irá se movimentar para cima da rampa para todos os itens). Adote .
a) Determine o valor do coeficiente de atrito cinético entre o bloco de e a rampa para que o sistema chegue à posição a com velocidade zero.
b) Assuma agora que o valor do coeficiente de atrito cinético é e que de novo o sistema é puxado à posição b e liberado a partir do repouso. Neste caso, determine o valor máximo de compressão da mola.
Ver solução completaQuestão 81
Um brinquedo consiste em um tubo inclinado de 30° em relação à horizontal contendo no fundo uma mola de constante elástica e uma bolinha de massa . Na posição , a mola está comprimida, e na posição a mola está relaxada e perde o contato com a bolinha. A mola é liberada arremessando a bolinha para fora do tubo. Fora do tubo, a bolinha descreve uma trajetória parabólica chegando a uma altura máxima . Suponha o atrito desprezível e responda às perguntas abaixo em função dos dados conhecidos do problema.
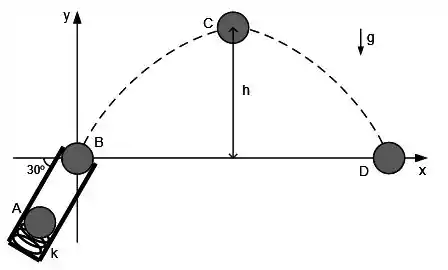
a) Usando conceitos de conservação de energia, determine o módulo da velocidade da bolinha quando ela passa pela origem do sistema de coordenadas da figura, ponto . Assuma que ela partiu do repouso.
b) Determine o tempo de permanência da bolinha no ar, entre os pontos e
c) Supondo a velocidade no ponto conhecida e utilizando a conservação de energia, escreva uma equação em função dos dados do problema que permita determinar a distância que a mola foi comprimida.
d) Considere agora que existe uma força de atrito do tubo que age na bolinha ao longo da distância enquanto ela vai da posição para a posição . Esta força de atrito varia linearmente com a distância, começando com o valor 0 (zero) na posição e chegando ao valor na posição . Calcule a variação da energia mecânica no trajeto.
Ver solução completaQuestão 82
Uma caixa desliza sobre uma superfície horizontal com velocidade escalar de quando, no ponto , encontra uma área áspera. Na área áspera, o coeficiente de atrito não é constante, mas se inicia a em e aumenta linearmente conforme ultrapassa , atingindo um valor de a após o ponto .
b) Qual é o coeficiente de atrito no ponto de parada?
Ver solução completaQuestão 83
Um bloco de massa inicialmente em repouso desliza para baixo em um plano inclinado que faz um ângulo com a horizontal. Depois de ter deslizado uma distância , o bloco colide com uma mola de constante elástica desconhecida. A mola reduz a velocidade do bloco até fazê-lo parar momentaneamente. Neste instante a mola está comprimida de uma distância . Não existe atrito entre o plano e o bloco até o contato com a mola (deslocamento ). Mas existe atrito entre plano e o bloco na região da mola (deslocamento ) com coeficiente de atrito cinético . Use para a aceleração da gravidade. Responda em função dos dados fornecidos utilizando a Lei de Conservação de Energia.
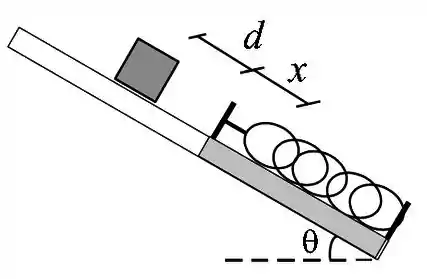
(c) Após ter sido toda comprimida, a mola empurra o bloco de volta plano acima e o bloco para momentaneamente a uma distância da mola quando ela está relaxada novamente. Determine a distância , em função das variáveis dadas.
Ver solução completaQuestão 84
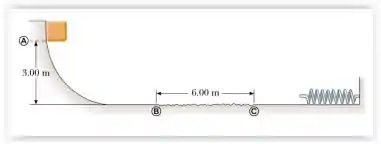
Um bloco com massa m = 10,0 kg é solto do repouso do ponto A da figura. O pavimento é sem atrito, exceto pelo trecho entre os pontos B e C, o qual tem comprimento 6,00 m. O bloco então atinge a mola, cuja constante elástica é k = 2250 N/m, e a comprime 0,300 m a partir da sua posição de equilíbrio. Qual o coeficiente de atrito cinético entre o bloco e o pavimento entre os pontos B e C?
(A) µc = 0,328
(B) µc = 0,432
(C) µc = 0,278
(D) µc = 0,156
(E) µc = 0,500
Ver solução completaQuestão 85
O deslocamento de uma carga da base de um plano inclinado até o topo é feito por um dispositivo análogo ao da figura ao lado. Ele é constituído por uma caixa, de massa , presa na extremidade de um cabo. O cabo passa por uma roldana no topo do plano inclinado e tem um contrapeso, de massa , em sua outra extremidade. Próximo ao topo existe uma mola de constante elástica . As superfícies da caixa e do plano inclinado são rugosas, com coeficiente de atrito cinético . O ângulo que o plano inclinado faz com a horizontal é 25°. Liberando o contrapeso a partir do repouso, a caixa é puxada pelo cabo. Ela pode transportar cargas de até , por uma distância , desde a base do plano até o ponto de máxima compressão da mola , quando então a caixa é parada pela mola, antes que o contrapeso chegue ao solo. Considere o cabo e a roldana ideais. Utilize ; e .
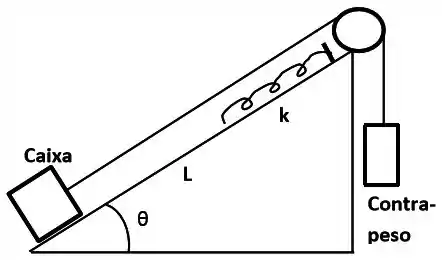
a) Use conceitos de trabalho e energia para obter a compressão máxima da mola em função de , , , , , , , e quando a caixa estiver com a carga máxima. Calcule o valor de .
b) Encontre a expressão teórica para a velocidade máxima da caixa. Utilize para a compressão máxima da mola e despreze o atrito neste caso. Responda em função das variáveis do problema.
Ver solução completaQuestão 86
Um bloco de massa está comprimindo em uma mola ideal de constante elástica . Ao ser liberado do repouso, o bloco se desprende da mola percorrendo um piso horizontal sem atrito, quando então passa a um trecho horizontal de comprimento que oferece atrito de coeficiente cinético igual a . O bloco tem à sua frente uma rampa lisa, na qual ele para momentaneamente a uma altura máxima, tornando a descer a rampa, a passar novamente pelo trecho com atrito, a comprimir a mola e assim sucessivamente, até parar definitivamente. Adote
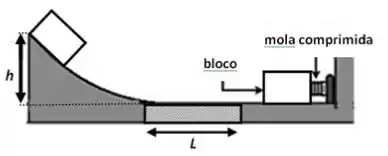
Determine:
(a) a variação de energia térmica do sistema bloco-piso na primeira vez que o bloco percorre completamente o trecho ;
(b) a maior altura que o bloco atinge na rampa;
(c) a compressão máxima da mola na primeira vez que o bloco retorna comprimindo-a;
d) a posição onde o bloco para definitivamente.
Ver solução completaQuestão 87
Uma partícula pode deslizar em uma pista com extremidades elevadas e uma parte central plana, conforme mostrado na figura. A parte plana tem um comprimento . Os trechos curvos da pista não possuem atrito, mas na parte plana o coeficiente de atrito cinético vale . A partícula é solta a partir do repouso no ponto , que está a uma altura . A que distância da borda esquerda da parte plana a partícula finalmente para?