Suponha que aponta para leste, aponta para o norte e aponta para cima. Determine os valores de (a) , (b) e (c) . Determine as orientações (como, por exemplo, para leste ou para baixo) dos produtos vetoriais (d) , (e) e (f) .
Passo 1
Vamos começar fazendo um desenho desses vetores:
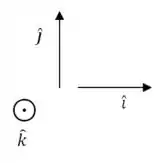
E aquele símbolo em cima do indica que ele é um vetor saindo do plano da página.
Passo 2
(a) Os vetores e são perpendiculares, então:
Passo 3
(b) Os vetores e também são perpendiculares:
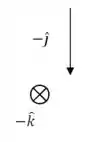
Então:
Passo 4
(c) Os vetores e são paralelos um ao outro, mas têm sentidos opostos:
Os dois tem o mesmo módulo, pois são vetores unitários:
E o ângulo formado por eles é de , então:
Passo 5
(d) Para descobrir a orientação de cada produto vetorial, temos que usar a regra da mão direita.
Em cada caso, você deve apontar o indicador na direçao do primeiro vetor, e o seu dedo médio na direção do segundo.
Depois que fizer isso, estenda o seu polegar. A direção do produto vetorial é a direção em que seu polegar está apontando.
Começamos com :
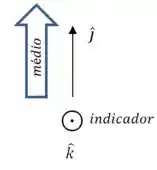
Nesse caso, seu polegar deveria apontar para oeste, no plano da página.
Passo 6
(e) Agora vamos analisar o caso de :
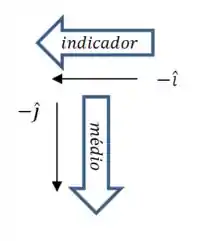
Nesse caso, seu polegar deveria apontar para fora da página (na direção que o enunciado chama de “para cima”).
Passo 7
(f) Por último, vamos considerar o caso de .
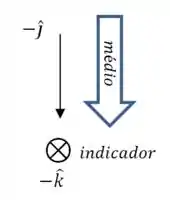
Mais uma vez, o seu polegar deve apontar para oeste.
Resposta
(a) Zero.
(b) Zero.
(c) .
(d) Oeste.
(e) Para cima.
(f) Oeste.