Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 1.Problemas - Ex. 13
13. Um bloco cúbico de aço, de de aresta e densidade , está mergulhando num recipiente com água, suspenso de uma balança de molas graduada em . A massa total do recipiente e da água é de , e ele está sobre um prato de uma balança, equilibrado por um peso de massa no outro prato (Fig . P.8). (a) Qual é a leitura da balança de molas? (b) Qual o valor de ?
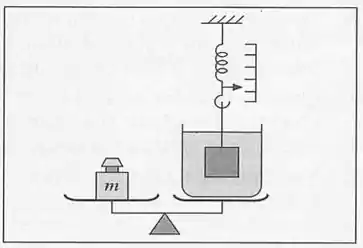
Passo 1
Bora lá pra mais um probleminha de hidrostática nesse maravilhoso e complicado livro de Física.
a) Bom! Esses é um clássico problema de equilíbrio de forças em hidrostática. Por isso vamos fazer o diagrama de corpo livre para o nosso recipiente com o bloco imerso em água:
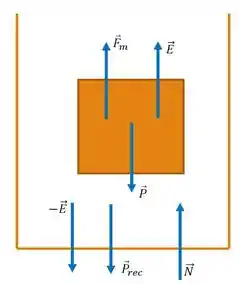
Como o sistema está em equilíbrio, temos então para o bloco a seguinte equação:
Onde representa a força exercida pela mola, o empuxo e o peso. Prosseguindo com os cálculos:
Onde representa a densidade da água, seu volume total e representa a densidade do bloco. Substituindo pelos valores fornecidos no enunciado, sabendo que o nosso bloco é um cubo, obtemos que:
Portanto, a leitura da balança é de :
Passo 2
b) Para este item, temos que a força exercida sobre o prato da balança do lado direito é a soma entre a força peso do recipiente e a água e a força de reação do empuxo entre o bloco e água, cuja direção é vertical e para baixo. Essa força deve se igualar ao peso do bloco de massa ... Portanto:
Resposta
a)
b)