Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 7.Problemas - Ex. 9

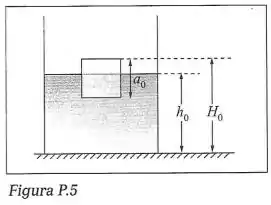
Um reservatório cilíndrico de aço contém mercúrio, sobre o qual flutua um bloco cilíndrico de latão. À temperatura de 20 ° C , o nível do mercúrio no reservatório está a uma altura h 0 = 0,5   m em relação ao fundo e a altura a 0 do cilindro de latão é de 0,3   m . A essa temperatura, a densidade do latão é de 8,60   g / c m 3 e a densidade do mercúrio é de 13,55   g / c m 3 . (a) Ache a que altura H 0 está o topo do bloco de latão em relação ao fundo do reservatório a 20 ° C (Fig. P5). (b) O coeficiente de dilatação linear do aço é 1,1 ⋅ 10 - 5 ° C - 1 ; o do latão é 1,9 ⋅ 10 - 5 ° C - 1 , e o coeficiente de dilatação volumétrica do mercúrio é 1,8 ⋅ 10 - 4 ° C - 1 . Calcule a variação δ H da altura H 0 (em m m ) quando a temperatura sobe para 80 ° C .

Passo 1

Esse é um problema com muitas informações que podem te deixar bem confusx! Ele parece misturar empuxo com dilatação, então vamos com bastante calma.

No item (a) estamos fixos à 20 ° C . Assim, não vamos precisar nos preocupar com a dilatação dos elementos do problema! Como o cilindro de latão está flutuando em equilíbrio, temos que seu peso se iguala ao empuxo:

P = E

Assim,

d l a t a o V c i l i n d r o   g = d m e r c u r i o   V l i q . d e s l   g

Lembre-se que para o peso nós usamos o volume do cilindro inteiro, enquanto para o empuxo nós devemos usar o volume do líquido deslocado, que no caso é o volume do cilindro submerso no líquido. Se A c for a área da base do cilindro e l 0 for a altura dele submersa, temos que

V c i l i n d r o = A c   a 0

V l i q . d e s l = A c   l 0

Assim,

d l a t a o   A c   a 0   g = d m e r c u r i o   A c   l 0   g

Simplificando A c e g :

l 0 = a 0   d l a t a o d m e r c u r i o

Passo 2

Note também que

H 0 = h 0 + a 0 - d = h 0 + a 0 - l 0

Portanto,

H 0 = h 0 + a 0 - a 0   d l a t a o d m e r c u r i o = h 0 + a 0 1 - d l a t a o d m e r c u r i o

Substituindo os valores:

H 0 = 0,5   m + 0,3   m ⋅ 1 - 8,60 13,55 = 0,6096   m

Assim,

H 0 = 60,96   c m

Passo 3

Agora, no item (b), a brincadeira vai ser um pouco diferente: vamos esquentar o sistema até 80 ° C e queremos saber o quanto a altura H 0 varia.

Vamos calcular primeiro o novo tamanho a do cilindro:

Δ a = a 0   α l a t a o   Δ T ⇒ a = a 0   1 + α l a t a o   Δ T

Se l for o novom comprimento submerso do cilindro após o aquecimento, segue valendo a relação

l = a   d l a t a o d m e r c u r i o 80 ° C = a 0   1 + α l a t a o   Δ T   d l a t a o d m e r c u r i o 80 °

Mas agora, as densidades também mudaram! O que não mudou foi a massa:

m = d 0   V 0 = d   V ⇒ d = d 0 V 0 V = d 0 V 0 V 0 ( 1 + 3 α Δ T ) = d 0 ⋅ 1 1 + 3 α Δ T

Assim,

d l a t a o d m e r c u r i o 80 ° = d l a t a o d m e r c u r i o 20 ° ⋅ 1 + γ m e r c u r i o Δ T 1 + 3 α l a t a o Δ T

Assim,

l = a 0   1 + α l a t a o   Δ T d l a t a o d m e r c u r i o 20 ° ⋅ 1 + γ m e r c u r i o Δ T 1 + 3 α l a t a o Δ T

Eu sei que tá ficando feio, mas vamos seguir em frente...

Passo 4

Por analogia com o item (a), teríamos

H = h + a - l

Tanto a como l já sabemos calcular. Se quisermos escrever uma expressão única:

H = h + a 0   1 + α l a t a o   Δ T - a 0   1 + α l a t a o   Δ T d l a t a o d m e r c u r i o 20 ° ⋅ 1 + γ m e r c u r i o Δ T 1 + 3 α l a t a o Δ T

Ou ainda,

H = h + a 0   1 + α l a t a o   Δ T   1 - d l a t a o d m e r c u r i o 20 ° ⋅ 1 + γ m e r c u r i o Δ T 1 + 3 α l a t a o Δ T  

O que falta é relacionar h com h 0 . Uma boa estimativa para isso é

h = h 0   1 + γ m e r c u r i o 3 - α a ç o Δ T

Na prática, temos que dividir o coeficiente de dilatação volumétrica do líquido pois estamos considerando a dilatação linear e o coeficiente do aço aparece subtraindo pois temos que considerar a diltação aparante devido ao recipiente. Note que

γ m e r c u r i o 3 - α a ç o Δ T = 1,8 ⋅ 10 - 4 3 - 1,1 ⋅ 10 - 5 ⋅ 60 = 4,9 ⋅ 10 - 5 ⋅ 60 = 2,94 ⋅ 10 - 3

Bom, uma variação de 10 - 3 em um meio metro não é tão desprezível quando queremos estudar variações de m m . Sendo assim, vamos considerar essa fator:

h = 0,5   m ⋅ 1 + 2,94 ⋅ 10 - 3 = 0,50147   m

Passo 5

Vamos agora olhar para o termo

1 - d l a t a o d m e r c u r i o 20 ° ⋅ 1 + γ m e r c u r i o Δ T 1 + 3 α l a t a o Δ T = 1 - 8,60 13,55 ⋅ 1 + 1,8 ⋅ 10 - 5 ⋅ 60 1 + 3 ⋅ 1,9 ⋅ 10 - 5 ⋅ 60 = 0,3668

Já para o outro termo

a = a 0   1 + α l a t a o   Δ T = 0,3   m ⋅ 1 + 1,9 ⋅ 10 - 5 ⋅ 60 = 0,300342   m

Note que as dilações dos comprimentos são bem desprezíveis perto das variações da densidade! Agora podemos achar H :

H = 0,50147   m + 0,300342   m ⋅ 0,3668

Assim,

δ H = H - H 0 = 0,50147   m + 0,300342   m ⋅ 0,3668 - 0,6096   m

Logo,

δ H = 0,00203   m = 2,03   m m

As respostas podem variar um pouquinho na primeira casa dependendo da sua hipótese para achar h !

Resposta

H 0 = 60,96   c m

δ H = 2,03   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Você está fervendo água para preparar uma massa. A receita diz que devem ser usados pelo menos 4,0 L de água. Você coloca os 4,0 L de água à temperatura ambiente dentro da panela e observa que esta qu
Estime a emissividade efetiva da Terra a partir da seguinte informação. A constante solar, que é a intensidade da radiação solar que incide na Terra, é cerca de 1,37 k W m 2 . Setenta por cento desta
Você está encarregado de cruzar o país transportando um fígado para uma cirurgia de transplante. O fígado é mantido frio em uma caixa de isopor inicialmente cheia com 1,0 kg de gelo. É crucial que a t
Considere o líquido de um barômetro cujo coeficiente de dilatação volumétrica é 6,6. 10 - 4/° C . Determine a variação relativa da altura do líquido se a temperatura variar de 12 ° C e a pressão perma
O calorímetro de fluxo é um dispositivo usado para medir o calor específico dos líquidos. O líquido que passa pelo calorímetro, com uma vazão conhecida, recebe energia, na forma de calor, a uma taxa c