Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 1.Problemas - Ex. 7
7. Um pistão é constituído por um disco ao qual se ajusta um tubo oco cilíndrico de diâmetro , e está adaptado a um recipiente cilíndrico de diâmetro . A massa do pistão com o tubo é e ele está inicialmente no fundo do recipiente. Despeja-se então pelo tubo uma massa de líquido de densidade ; em consequência, o pistão se eleva de uma altura . Calcule .
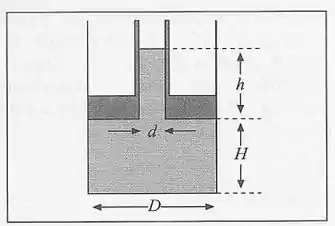
Passo 1
Bora lá pra mais um probleminha nesse maravilhoso e complicado livro de Física.
Olha só! Nos estamos trabalhando com um recipiente cilíndrico que acopla em seu interior um tubo cilíndrico. Ou seja, a primeira coisa que temos de fazer é obter a área compreendida pela base do pistão, que é dada por:
E como nós sabemos; a pressão exercida sobre uma superfície é a divisão da força atuante, no caso a força peso, pela área dessa superfície. Sendo assim...
Passo 2
Só que a nossa questão menciona que esse nosso sistema está em equilíbrio. E o que isso quer dizer, afinal de contas?
Ora bolas, que dizer que essa pressão que obtivemos no deve se igualar à pressão da coluna de água, dada pelo produto da densidade da água pela altura da coluna e a gravidade... Ficamos então, com a seguinte igualdade:
Isolemos, em seguida, esse :
Pronto! Achamos ! Vamos guardar ele a sete chaves, pra usar quando for a hora.
Passo 3
O que acha agora, de obtermos o valor da massa total de líquido presente no nosso sistema. Moleza, né? Basta fazer o produto da densidade pelo volume de água .
E como podemos ver no enunciado, o volume é dado por...
O que nos eleva até:
Por fim, só falta isolar esse :
E lembra lá do valor de no final do ... Pois é, ele vai cair aqui:
E fim! Resposta encontrada!