Um bloco escorrega para baixo com velocidade constante em um plano inclinado de ângulo . Em seguida, o bloco é lançado para cima no mesmo plano com velocidade inicial . (a) Que distância o bloco sobe até parar? (b) Depois de parar, o bloco torna a escorregar para baixo? Justifique sua resposta.
Passo 1
Vamos iniciar este problema fazendo o DCL do bloco quando ele escorrega para baixo:
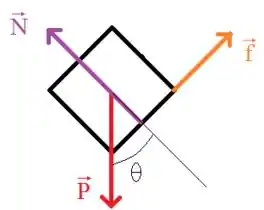
A partir da ilustração, podemos aplicar a segunda lei de Newnton para cada eixo:
Igualamos a zero, porque neste primeiro momento o bloco desce o plano inclinado com velocidade constante e, portanto, a aceleração é nula, .
Lembrando que a força de atrito cinético pode ser calculada a partir da seguinte relação:
Passo 2
A partir das equações acima, podemos determinar o valor do em função do ângulo . Para isso, vamos reescrever a usando a :
Substituindo a expressão acima na :
Dividindo os dois lados por e isolando :
Passo 3
Agora, vamos fazer o DCL do bloco quando está subindo o plano inclinado:
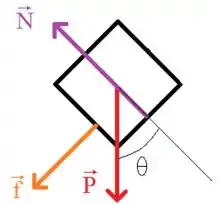
Aqui, podemos perceber que não há mais o equilíbrio das forças o eixo , portanto, aplicando a segunda lei de Newton:
Passo 4
Reescrevendo a em função das expressões já calculadas para , temos:
Dividindo tudo por :
Passo 5
Como a aceleração calculada é constante, podemos usar a equação de Torricelli para determinar a distância percorrida até parar:
Sabendo que , pois queremos a distância até o bloco PARAR, foi dado no enunciado e a aceleração foi calculada no passo anterior, podemos isolar :
Passo 6
A partir da que mostra o equilíbrio entre a componente do peso paralela ao plano inclinado e a força de atrito cinético, podemos interpretar que como a força de atrito estático é maior do que a força de atrito cinético, uma vez em repouso, este só irá se mover caso ocorra sobre ele uma outra força externa para coloca-lo em movimento. Como neste caso, não nenhuma outra força externa, então o bloco não descerá, portanto, permanecerá em repouso.
Resposta
- ;
- .