Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 8.Problemas - Ex. 3
Um bloco de gelo de tonelada, destacado de uma geleira, desliza por uma encosta de de inclinação com velocidade constante de . O calor latente de fusão do gelo (quantidade de calor necessária para liquefação por unidade de massa) é de . Calcule a quantidade de gelo que se derrete por minuto em consequência do atrito.
Passo 1
Conforme o bloco desce pelo plano, a força de atrito realiza trabalho. Vamos começar calculando esse trabalho.
As forças agindo sobre o bloco são as seguintes:
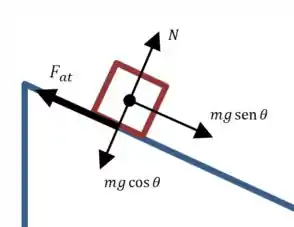
Já que o bloco se move com velocidade constante, as forças estão em equilíbrio em todas as direções. Então:
E se é a distância percorrida pelo bloco em certo intervalo de tempo, então o realizado pela força de atrito nesse trajeto é:
Como o bloco se desloca por a cada segundo, então o trabalho realizado pelo atrito a cada segundo é:
Passo 2
Mas o enunciado pediu para calcularmos a massa de gelo que é derretida a cada minuto por essa energia que acabamos de calcular.
Se o bloco recebe uma energia a cada segundo, então em um minuto temos:
E se essa energia é toda utilizada para derreter o gelo, então a massa de gelo derretida segue a seguinte relação:
Onde é a massa de gelo derretia de é o calor latente de fusão do gelo. Precisamos converter para joules por quilograma:
Então:
Agora podemos substituir os valores numéricos.
Resposta
de gelo são derretidas a cada minuto.