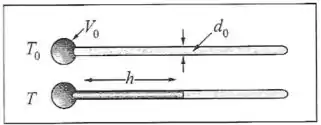
Para construir um termômetro de leitura fácil, do ponto de vista prática (Problema 7), acopla-se um tubo capilar de vidro a um reservatório numa extremidade do tubo. Suponha que, à temperatura , o mercúrio está todo contido no reservatório, de volume , e o diâmetro do capilar é . (a) Calcule a altura do mercúrio no capilar a uma temperatura (figura). (b) Para um volume do reservatório , calcule qual deve ser o diâmetro do capilar em para que a coluna de mercúrio suba de quando a temperatura aumenta de . Tome para o vidro e para o mercúrio.

O volume no reservatório (que fica sempre cheio) vai variar de acordo com o triplo do coeficiente de dilatação linear:

Já o volume líquido no capilar vai depender da área da secção e da altura preenchida:

E o diâmetro vai dilatar de acordo com o coeficiente :

Então:

Nosso objetivo é calcular a variação da altura em função da temperatura, então vamos isolar na nossa fórmula:

Vamos colocar em evidência do lado esquerdo da equação:

E como é um número muito pequeno, nós podemos fazer a seguinte aproximação:

Então:

Onde usamos .

(b) Agora queremos calcular o valor de dados , , e .

Só precisamos reorganizar um pouco a fórmula que acabamos de encontrar:

Então, usando todos os comprimentos em centímetros:

Convertendo para milímetros: