Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 10.7 - Ex. 41
O bloco homogêneo da figura abaixo, tem massa 0,172 Kg e lados a=3,5 cm, b=8,4 cm e c=1,4 cm. Calcule o momento de inercia do bloco em relação a um eixo que passa por um canto e é perpendicular às faces maiores.
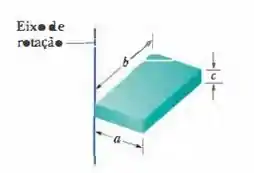
Passo 1
Por se tratar de um bloco em relação a um eixo que não passa pelo seu centro, então podemos usar o Teorema dos eixos paralelos:
Onde é o momento de inércia com relação ao eixo de rotação na extremidade da placa, é o momento de inércia de uma placa com relação ao centro de massa, é a massa da placa e
É a distância entre os dois eixos.
Sendo a distância entre o centro de massa e o eixo de rotação, então:
Além disso, o momento de inércia da placa com relação ao centro de massa é tabelado e será:
Belezinhaa?!
Então vamos lá!!!
Passo 2
Como temos:
Então podemos substituir as expressões de e :
Show de bola?!
Podemos simplificar a expressão para facilitar nossa vida. Desse jeito:
Colocando tudo no mesmo denominador vamos obter que:
Logo:
Passo 3
Agora é só substituir os valores dados no problema, de modo que::
