Enunciado
Física - Hibbeler - Estática- Ed: 14º - Capítulo 10.Problemas - Ex. 31
Determine a localização do centroide da área da seção transversal do canal e depois calcule o momento de inércia da área em relação a esse eixo.
Passo 1
Fala aí, galerinha do Responde aí. Tudo beleza? Vamos fazer mais uma questão de Estática.
Este problema nos pede para determinarmos o centroide e o momento de inercia em relação ao eixo para esta viga.
Primeiro, temos que determinar o centroide desta viga. Para um corpo composto ele é dado por:
Assim, as áreas dos segmentos e seus respectivos centróides estão tabulados abaixo:
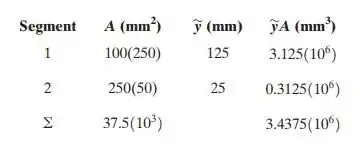
Assim, o centroide vai ser:
Passo 2
Em seguida, vamos determinar o momento de inércia sobre o eixo . Sabemos que o momento de inercia em para cada segmento pode ser determinado usando o teorema dos eixos paralelos:
Por tabela, temos:
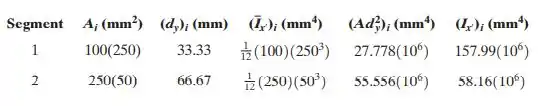
Sabemos que o momento de inercia para corpos compostos é dado por:
𝐼𝑥′=𝑥′𝑖=×106 𝑚𝑚4
É isso, galera, Bora resolver mais questões pra ficar craque.