Exercícios de Teorema dos Eixos Paralelos - Lista de Exercícios Resolvida
Questão 1
Uma esfera oca e rígida de massa e raio tem momento de inércia relativo a um eixo que passa pelo seu centro de massa. Relativamente a um eixo que tangencia a periferia da esfera e é paralelo ao eixo que passa pelo centro de massa, o momento de inércia da esfera é
Questão 2
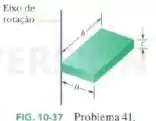
O bloco uniforme da Fig. 10-37 tem massa de e lados , e . Calcule o momento de inercia do bloco em relação a um eixo que passa por um canto e é perpendicular às faces maiores.
Questão 3
Calcule o momento de inércia de uma régua de um metro, com uma massa de , em relação a um eixo perpendicular à uma régua na marca de . (Trate a régua como uma barra fina.)
Ver solução completaQuestão 4
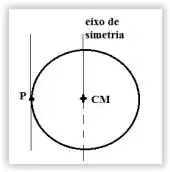
O momento de inércia de um anel em torno de seu eixo de simetria é. Qual é o momento de inércia em relação ao eixo P paralelo ao eixo de simetria que passa pela borda do anel?
A) 5
B) 2
C)
D) 1,5
E) 0,5
Ver solução completaQuestão 5
Uma placa metálica fina de massa tem forma retangular com lados e . Use o teorema dos elementos paralelos para determinar seu momento de inércia em relação a um eixo perpendicular ao plano da placa passando por um dos seus vértices.
Ver solução completaQuestão 6
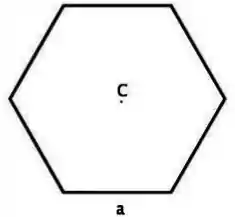
Uma haste fina e uniforme com uma massa é dobrada para formar um hexágono regular de lado . Qual é o momento de inércia do hexágono em torno do eixo que passa pelo seu centro e é perpendicular ao plano formado pelo hexágono? Considere que o momento de uma haste fina de comprimento é dado por .
Questão 7
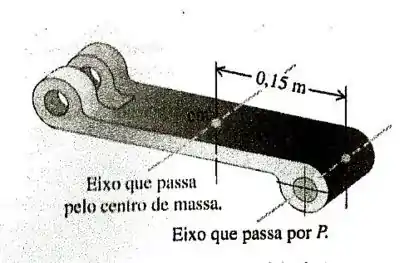
Uma das peças de uma articulação mecânica possui massa igual a . Medimos seu momento de inércia em relação a um eixo situado a uma distância de do seu centro de massa e encontramos o valor . Qual é o momento de inércia em relação a um eixo paralelo que passa pelo centro de massa?
Ver solução completa
Questão 8
Um objeto quadrado de massa é formado de quatro varetas finais idênticas, todas de comprimento e massa , amarradas juntas. O objeto é fixado a uma barra, podendo girar em torno dela com velocidade angular , como mostrado na figura. O momento de inércia do objeto em relação ao eixo de rotação na figura é:
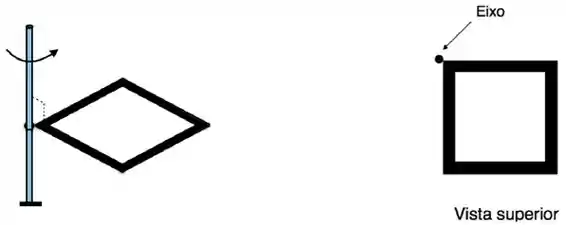

Questão 9
Na figura abaixo são dadas duas esferas de igual massa e igual raio , porém a da esquerda é maciça (cheia) e homogênea e a esfera da direita é oca (sua massa está toda numa casca esférica de espessura desprezível).

A primeira esfera é posta para girar ao redor de um eixo deslocado de uma distância em relação a um de seus diâmetros. É possível, nestas condições, a segunda esfera apresentar um momento de inércia de valor aproximadamente igual ao da primeira?
Não, a esfera cheia apresenta maior momento de inércia que a oca já no caso , e deslocar o eixo para longe do centro de massa só iria aumentar seu momento de inércia.
Sim, mas só quando
Sim, mas só quando
Sim, mas só quando
Sim, mas só quando
Ver solução completaQuestão 10
Uma partícula de massa kg move-se inicialmente com velocidade m/s em um plano horizontal sem atrito (ver Figura). Uma barra delgada e homogênea, de massa kg e comprimento m, repousa inicialmente sobre este mesmo plano. A barra pode girar sem atrito ao redor de um eixo fixo, perpendicular ao plano horizontal e que passa pelo ponto numa extremidade da barra. Em um dado instante, a partícula colide com o centro
da barra, perpendicularmente a ela, e fica grudada. O sistema barra + partícula passa então a girar ao redor do ponto .
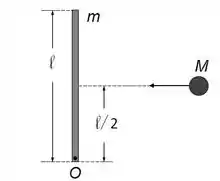
Qual é o momento de inércia da barra em relação a um eixo perpendicular a ela e que passa pelo ponto ? Dado: Momento de inércia da barra em relação a um eixo perpendicular a ela e que passa pelo seu centro de massa: .
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Ver solução completaQuestão 11
Uma esfera oca e rígida de massa e raio tem momento de inércia relativo a um eixo que passa pelo seu centro de massa. Relativamente a um eixo que tangencia a periferia da esfera e é paralelo ao eixo que passa pelo centro de massa, o momento de inércia da esfera é
Questão 12
Um eixo é espetado no centro de massa de uma garrafa, perpendicularmente ao comprimento. Nesta situação, o momento de inércia medido experimentalmente é . Quando o eixo é deslocado paralelamente para um ponto O, a uma distância de do centro de massa, o momento de inércia medido é . A massa da garrafa é:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Ver solução completaQuestão 13
Uma haste longa e fina de massa e comprimento é livre para girar sobre um ponto localizado a de seu comprimento. A haste é posicionada na posição horizontal, como mostrado na figura , por um fio preso na extremidade:
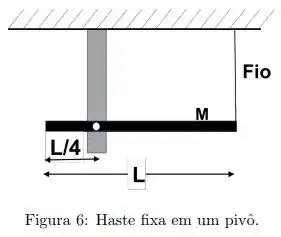
(a) Dado que o momento de inércia em relação ao eixo de rotação perpendicular a haste e passando pelo centro de massa é , determine o momento de inércia da haste relativo ao pivô de rotação em .
Ver solução completaQuestão 14
Considere as seguintes afirmações:
I. Um corpo em rotação livre (não sujeito a forças externas) gira em torno do centro de massa.
II. O centro de massa de um corpo rígido é um ponto do corpo.
III. O momento de inércia de um corpo rígido depende somente da posição do eixo de rotação e da massa total do corpo.
É (são) verdadeira(s) a(s) afirmação(ões)
(A) I, II e III
(B) I e III
(C) II e III
(D) I
(E) III
Ver solução completaQuestão 15
O momento de inércia de uma barra homogênea de massa m e comprimento l em relação a um eixo que passa por uma de suas extremidades e é perpendicular a ela é . Uma barra homogênea de comprimento L e massa M é dobrada a uma distância L/3 de uma de suas extremidades, como mostra a figura. O momento de inércia desta configuração em relação ao eixo Oy é:
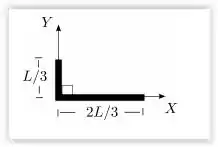
Questão 16
Dado que a massa da terra é , o raio da terra é , a massa da lua é , a distancia entre a terra e a lua é . Determine a que distância do centro de massa do sistema Terra-Lua está do centro da Terra? Expresse sua resposta como uma fração do raio da Terra.
Escolha uma opção:
- 0,58
- 0,86
- 1,83
- Nenhuma das alternativas
- 1,26
- 1,58
- 0,73
Questão 17
Uma placa homogênea que era quadrada tem sua área reduzida de um quarto, conforme a figura.
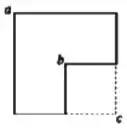
Os momentos de inércia em relação a eixos perpendiculares ao plano da placa e que passam pelos pontos , e são, respectivamente, , e . Pode-se afirmar que:
Questão 18
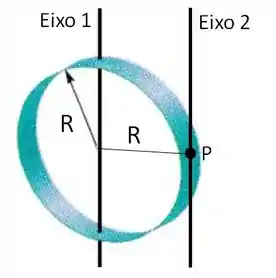
Considere o anel de raio e massa total , desenhado na figura abaixo. O momento de inércia com relação a um eixo que passa por seu ponto de centro de massa e é paralelo ao plano do anel, conforme a figura, é . Determine o momento de inércia com relação a um segundo eixo que é paralelo ao primeiro, mas que passa pelo ponto conforme a figura.
A.
B.
C. .
D.
E.
Ver solução completaQuestão 19
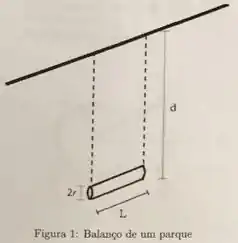
Um balanço de parque é formado por uma barra cilíndrica de massa , raio , e comprimento , preso por fios de massa desprezível a um eixo fixo superior, paralelo ao eixo da barra cilíndrica, conforme a figura 1. A barra pode girar em torno desse eixo fixo. O centro da barra está a uma distância do eixo. O momento de inércia da barra com relação ao eixo fixo vale:
Dados de Momento de inércia:
Disco uniforme (massa , raio )com relação a um eixo que passa pelo seu centro de massa e é perpendicular ao plano do disco: .
Barra uniforme (massa , comprimento ) com relação ao eixo que passa pelo seu centro de massa e é perpendicular ao comprimento da barra: .
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 20
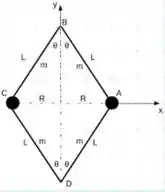
. O sistema mostrado na Figura é formado por quatro barras iguais de massa e comprimento e por duas massas pontuais iguais de massa presas às barras nos pontos e . Sabe-se que o momento de inércia de uma barra que forma um o ângulo com o eixo de rotação que passa pelo seu centro de massa é , . Determine o momento de inércia do sistema em torno do eixo .
Questão 21
(Cap 10.7 – Ex. 35) Calcule o momento de inércia de uma régua de um metro, com uma massa de , em relação a um eixo perpendicular à régua na marca de. (Trate a régua como uma barra fina.)
Ver solução completaQuestão 22
. Sete moedas estão organizadas hexagonalmente de tal forma que que cada moeda encosta em sua vizinha como mostrado na figura. Cada moeda é um disco uniforme de raio e massa . Qual é o momento de inércia do sistema de sete moedas em relação a um eixo que passa no centro da moeda central e é normal às moedas?
Ver solução completaQuestão 23
Uma porta retangular homogênea de 25 kg tem 220 cm de altura e 91 cm de largura. Qual o momento de inércia da porta para rotações em torno de:
a) um eixo paralelo o seu lado mais longo que passa pelas dobradiças
b) um eixo paralelo ao seu lado mais longo que passa a uma distância de 15 cm das suas dobradiças.
Ver solução completaQuestão 24
Calcule, por integração direta, o momento de inércia de um bastão de massa M e comprimento L em torno de um eixo que passa a uma distância d de uma de suas extremidades. Compare o seu resultado com tabelas de momentos de inércia para os casos particulares d=0 e d=L/2.
Ver solução completaQuestão 25
Um quadrado de massa e de lados de comprimento , tem um momento de inércia , quando rodado em torno de um eixo perpendicular à sua superfície, e que passa por uma de suas extremidades, como mostrado na figura. Agora, uma partícula, também de massa está ligada a um canto do quadrado, como mostrado. Qual é o novo momento de inércia do sistema sobre o mesmo eixo de rotação?

a)
b)
c)
d)
e)
Ver solução completaQuestão 26
Um disco metálico homogêneo de raio tem um furo circular de raio conforme a figura abaixo.
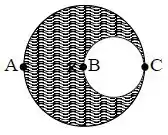
Três eixos paralelos entre si e perpendiculares ao disco passam pelos pontos , e da figura. A posição do centro de massa é representada por um na figura.
Os momentos de inércia do objeto em relação a cada um desses eixos são, respectivamente, , e .
Determine a alternativa correta:
- ;
- ;
- ;
- ;
- ;
- .
Questão 27
Um disco de raio e massa e um cubo de lado e mesma massa, estão no topo de um plano com comprimento inclinado de com a horizontal. Existe atrito entre o plano inclinado e os dois objetos, os coeficientes de atrito cinético e atrito estático são respectivamente e . Na base do plano existe um trilho na vertical com o formato de um anel de raio como ilustra o desenho. A base do plano e o trilho têm superfícies com atrito desprezível. Na saída do trilho, está em repouso um segundo cubo idêntico ao primeiro com seu centro de massa na posição . Logo após o segundo cubo, a superfície horizontal apresenta um coeficiente de atrito cinético variável e no final desta superfície está uma mola com constante elástica . A superfície embaixo da mola tem atrito desprezível. A origem do sistema de coordenadas coincide com o centro do anel. A aceleração da gravidade é . Desenvolva as equações na forma literal para somente no final substituir as variáveis pelos valores fornecidos.
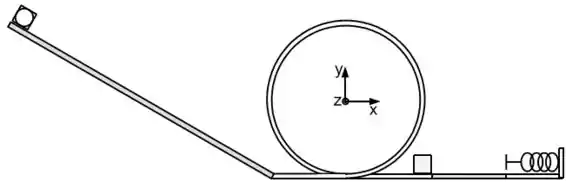
b) Calcule o momento de inercia rotacional do disco em relação ao ponto de contato com o plano inclinado.
Ver solução completaQuestão 28
Cada sistema e é composto de um disco, uma haste presa ao disco e duas massas presas `a haste. A haste está contida no plano do disco. Um bloco é preso à extremidade livre de um fio leve enrolado ao redor do disco que pode girar livremente em torno do eixo que passa pelo seu centro e é perpendicular ao seu plano. Os dois sistemas mostrados na figura abaixo são idênticos, exceto pelas posições das massas na haste. Se os dois blocos são soltos simultaneamente a partir do repouso, qual deles chega primeiro ao solo? E por que?
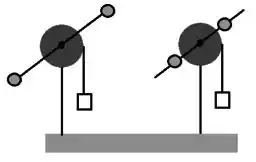
O do sistema , porque neste o momento de inércia é maior do que o de .
O do sistema , porque neste o momento de inércia é menor do que o de .
O do sistema , porque neste o momento de inércia é menor do que o de .
O do sistema , porque neste o momento de inércia é maior do que o de .
Os dois blocos chegam ao mesmo tempo.
Ver solução completaQuestão 29
Um objeto é formado por quatro barras delgadas homogêneas, cada uma com massa e comprimento , na forma de um quadrado. O momento de inércia em relação ao eixo representado pela linha pontilhada na figura e passando pelo plano do objeto é:
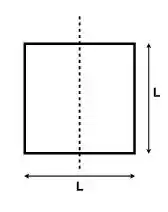
(a)
(b)
(c)
(d) nenhuma das alternativas
(e)
Ver solução completa