Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 7.6 - Ex. 22
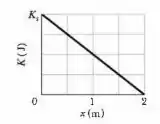
Um bloco é lançado para cima em uma rampa sem atrito, ao longo de um eixo que aponta para cima . A Fig. 7-30 mostra a energia cinética do bloco em função da posição ; a escala vertical do gráfico é definida por . Se a velocidade inicial do bloco é, qual é a força normal que age sobre o bloco?
Passo 1
Oi, querido! Tudo bem?
Então, a gente tem um bloco que é lançado em uma rampa. Algo assim:
O eixo aponta para cima.
Aí repara que o gráfico que dá a energia cinética do bloco em função de , diz que na posição máxima de , a energia cinética é nula. E isso faz sentido, porque em máximo estamos na altura máxima onde , e quando a velocidade é 0, a energia cinética é .
Então o bloco começa em com uma aceleração não nula de valor e chega na altura máxima com . Logo, ele fica sobre efeito de uma aceleração negativa.
Bem, o que ele quer saber nessa situação toda é o valor da força normal sobre o bloco.
Passo 2
Vamos fazer o diagrama de corpo livre do bloco durante o movimento:
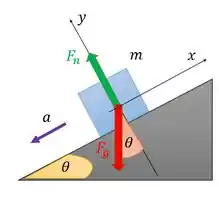
Vamos aplicar a segunda lei de Newton para o eixo :
Não temos movimento nessa direção, então . E as forças que temos nessa direção são a componente de em para baixo e a força normal (que a gente quer achar) para cima :
Percebe que a força normal que a gente quer achar é a componente vertical da força peso. Guarda essa informação no coração.
Passo 3
A gente sabe que o módulo da força peso é
E também o módulo dessa força pode ser calculado usando a fórmulinha de módulo:
Vamos igualar as duas e substituir o que a gente achou no passo anterior :
Podemos isolar quem a gente quer:
Percebe que a gente não tem duas coisas nessa expressão. Não temos a massa do bloco e nem a componente . E agora?
Passo 4
A gente não usou o gráfico que ele deu ainda né? É agora que ele começa a ser útil!
Ele diz que a energia cinética inicial em é , e a gente sabe a velocidade inicial também!
Aí para uma energia cinética inicial e , podemos achar a massa do bloco através da fórmulinha de energia cinética:
Sendo assim :
Passo 5
Agora falta . Olha nosso diagrama de novo:
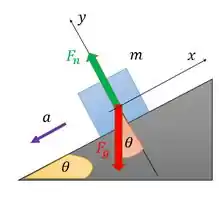
Quem gera a aceleração negativa do bloco é o somatório das componente das forças que atuam sobre o bloco.
Percebe que a única força com componente na direção é a força peso. Ou seja, quem causa é . Em outras palavras, quem está na direção do movimento é apenas. E assim, ela gera trabalho sobre o bloco para reduzir sua velocidade.
E o trabalho de uma força constante é dado por
Para a nossa força seria:
Negativa porque ela se opõe ao movimento. A gente vê pelo gráfico que o deslocamento do bloco é :
Passo 6
Mas por que raios a gente colocou em função do trabalho realizado??
Cara, porque a gente sabe a energia cinética inicial e final pelo gráfico, e aí pelo teorema trabalho-energia cinética a gente consegue relacionar essas energia com . Olha a carinha desse teorema:
Pelo gráfico e :
Substituindo isso em :
Passo 7
Agora temos tudo para achar :
Substituindo o que a gente achou aí e :
Resposta
Atenção! Cientistas afirmam que o próximo exercício tem 117,3% de chances de cair na sua prova , não deixem de conferir