Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 11.Exercícios e Problemas - Ex. 70
Em cada um dos Problemas de 69 a 72, é fornecida uma ou mais equações para resolver um problema. Em cada um deles, você deve
a. Redigir um problema realista para o qual a(s) equação(ções) seja(m) apropriada(s).
b. Desenhar uma representação pictórica correspondente.
c. Resolver o problema proposto.
70.
Passo 1
Opa! Aqui vamos nós de novo!
a) Olha só! Aquele ali na fórmula de novo! Pelo exercício anterior, já sabemos que se trata de coeficiente de atrito.
E temos uma distância de ali, que tá sendo multiplicada pelo seno e pelo cosseno de . Isso tá com cara de plano inclinado.
Como temos também apenas uma velocidade num instante e ela está ao quadrado, significa que a outra velocidade supostamente, no estado vai estar em repouso.
Pronto! Matamos o problema!
Acho que com esse três dados importantes! Dá pra ver que o problema basicamente vai ser um corpo descendo um plano inclinado.
Não esquecendo que pela equação, podemos tirar que a massa do corpo é de e pelo jeito, vai descer apenas devido ao efeito da aceleração da gravidade
Desse modo! Propomos o seguinte problema...
“Um caixote de desliza por uma rampa de de altura e da parte traseira de um caminhão até o chão. O coeficiente de atrito cinético entre a caixa e a bancada da rampa é de Qual a rapidez com que o caixote vai para o fundo da rampa?”
b) E aqui está um esboço pra ajudar melhor na compreensão do problema...
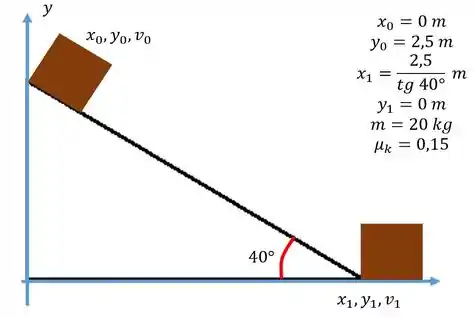
Passo 2
c) Feito o esboço, bora fazer o diagrama de corpo livre para o nossa caixote enquanto está no plano...
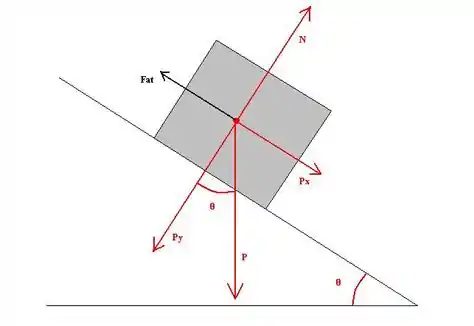
Uma vez que a caixa se move para baixo, a força resultante também apontará para a direita. No caso, a força peso é no sentido do movimento e a força de atrito se opõe ao movimento.
Com isso, vamos utilizar o Teorema Trabalho e Energia, que diz que a variação de energia cinética é igual ao trabalho da força externa resultante
Substituindo os valores que temos...
Como pode-se ver, chegamos exatamente até a equação proposta! Resolvendo-a...
Obtemos finalmente nossa resposta!
Resposta
a)
“Um caixote de desliza por uma rampa de de altura e da parte traseira de um caminhão até o chão. O coeficiente de atrito cinético entre a caixa e a bancada da rampa é de Qual a rapidez com que o caixote vai para o fundo da rampa?”
b)
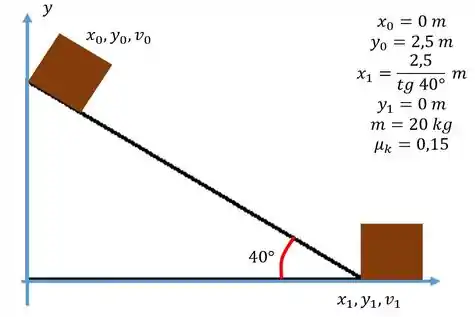
c)