Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 13.1 - Ex. 81
Um bloco de madeira de flutua na água, com de seu volume submerso. Um bloco de chumbo é colocado na madeira, submergindo completamente a madeira a uma profundidade em que o chumbo permanece totalmente fora da água. Encontre a massa do bloco de chumbo.
Passo 1
Opa, e aí, tudo firmeza? Espero que sim, bora solucionar mais uma questão? Queremos a massa do bloco de chumbo. Para isso a gente vai fazer análise do equilíbrio de forças nas duas situações que ele mostra.
Bem, olha só, inicialmente, a gente tem esse sistema aqui:
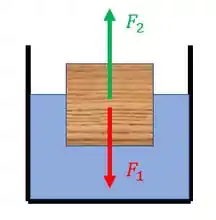
Como o bloco, de massa , tá flutuando (está parado), as forças representadas tem o mesmo módulo (estão em equilíbrio):
Sendo a força peso e o empuxo (), chegamos na equação:
E pelo princípio de Arquimedes, temos que o empuxo vale:
Substituindo isso na nossa equação
Passo 2
Agora pensa comigo: se do volume do bloco está submerso, esse é exatamente o volume de água que foi deslocada! Pô, a equação ganha a seguinte cara:
Onde é o volume do bloco de madeira.
Podemos achar uma expressão para o volume do bloco, através da fórmula para a densidade dele:
A nossa equação fica:
Vamos guardar isso por enquanto, beleza? Segue o baile.
Passo 3
Num segundo momento, nosso sistema passa a ser. Vamos considerar que e são forças que atuam no sistema bloco de madeira +bloco de chumbo.
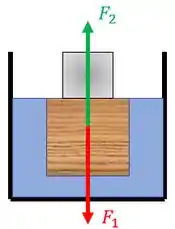
Como aqui também temos uma situação de repouso, e representando o peso do sistema bloco de madeira bloco de chumbo, vamos ter a seguinte equação:
Percebe que novamente representa o empuxo. Podemos então substituir a fórmula desse cara na nossa equação
Agora, calma. O empuxo só se importa com a quantidade de água deslocada. Como o bloco de madeira inteiro está submerso dessa vez, o volume de água deslocada é o volume inteiro do bloco de madeira apenas:
Percebe que o bloco de chumbo não influenciou o empuxo, isso porque ele não emerso (não tem nenhuma porcentagem dentro da água.
Passo 4
Agora temos um momento muito bonito. Lá do passo 2 anterior, achamos:
Substituindo isso na nossa equação do passo 3
E como, para o bloco de madeira, podemos escrever:
Vamos ter:
E ta na mão pessoal! A massa do bloco de madeira é um dado do enunciado! Vamos ter: