Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 9ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 9º - Capítulo 14.7 - Ex. 65
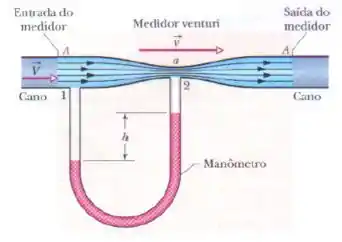
Um medidor venturi é usado para medir a velocidade de um fluido em um cano. O medidor é ligado entre dois segmentos do cano (Figura); a seção reta na entrada e na saída do medidor é igual à seção reta do cano. Entre a entrada e a saída do medidor o fluido escoa com velocidade e depois passa com velocidade por uma “garganta” estreita de seção reta . Um manômetro liga a parte mais larga do medidor à parte mais estreita. A variação da velocidade do fluido é acompanhada por uma variação da pressão do fluido, que produz uma diferença na altura do líquido nos dois lados do manômetro. (A diferença corresponde à pressão na garganta menos a pressão no cano.) (a) Aplicando a equação de Bernoulli e a equação de continuidade aos pontos e na figura, mostre que
Onde é a massa específica do fluido. (b) Suponha que o fluido é água doce, que a seção reta é no cano e 32 na garganta, e que a pressão é no cano e na garganta. Qual é a vazão de água em metros cúbicos por segundo?
Passo 1
Belezoca galerinha, a letra (a) já diz que vamos ter que usar a equação de Bernoulli e a equação da continuidade pra demonstrar aquela equação.
A equação de Bernoulli é dada como:
E a da continuidade diz:
Outra dica que o enunciado dá é que a diferença de pressão entre a parte mais apertada e a parte mais folgada do cano é o que produz a diferença de pressão no tubo em U, e o desnível nele. Então bora lá ver como fica essa brincadeira ai...
Passo 2
Então vamos aplicar a equação de Bernoulli a esses dois pontos: o mais apertado (vamos dizer que esse é o ponto ), e o mais folgado (vamos dizer que esse é o ponto ).
Vamos juntar alguns termos:
O cano principal é reto, certo? Então não tem nenhuma diferença de altura, por isso , e a equação fica assim:
E essa diferença de pressão? Bem, a fórmula final que eles querem que a gente demonstre inclui esse termo, então vamos deixar ele quieto, só trocando o nome :
Esse é a velocidade na parte mais apertada, que a questão chama de (minúsculo) e o é a velocidade na parte mais larga, que a questão chama de (maiúsculo). Vamos substituir e isolar o .
Agora falta substituir essa velocidade .
Passo 3
Aproveitando a dica do enunciado, vamos usar a equação da continuidade. Sabendo que a área maior é (maiúsculo) e a área menor é (minúsculo)
Substituindo na equação de cima:
Logo:
Tal que:
Pronto, está demonstrado!
Passo 4
A letra (b) basicamente dá um monte de números que podemos substituir na equação que acabamos de achar.
Como o fluido é água doce, podemos usar a densidade . O enunciado também dá , e .
A questão também dá as duas pressões:
Substituindo tudo:
Passo 5
Ainda não acabou, a questão pede a vazão em metros cúbicos por segundo. Vamos lembrar que isso é exatamente o que aquele produto da equação da continuidade dá.
Ou seja, se chamarmos a vazão de , vamos ter:
Pronto, agora sim acabou.
Resposta
(a) Demonstração
(b)