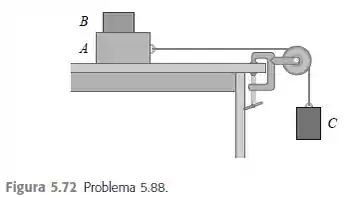
Um bloco de massa de está sobre um bloco de massa de , que por sua vez está sobre o topo de uma mesa horizontal (Figura ). Não há atrito entre o bloco e o topo da mesa, mas o coeficiente de atrito cinético entre o bloco e o topo da mesa é . Um fio leve ligado ao bloco passa sobre uma polia fixa sem atrito e o bloco está suspenso na outra extremidade do fio. Qual deve ser o maior valor da massa que o bloco deve possuir para que os blocos e deslizem juntos quando o sistema for libertado a partir do repouso?

Vamos começar pelo mais simples, o bloco , onde só temos atuando a força peso e a tensão da corda:

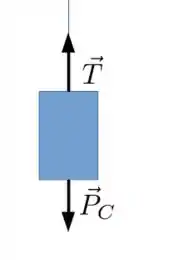
A segunda lei de Newton pra esse bloco fica

Onde é a tração da corda, é o peso do bloco e é a aceleração da gravidade.

Agora vamos olhar para o bloco . A princípio teríamos somente o peso e a normal, maaass tem o atrito entre o bloco e o bloco ! Em que direção aponta esse atrito?

Bem, se os dois blocos andam juntos, então é esse atrito que faz o bloco andar para frente, certo? O diagrama fica assim

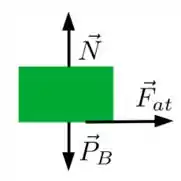
Onde é a força de atrito, é a normal e é o peso do bloco B.

OBS: tem que ser atrito estático por que o bloco não arrasta quando está sobre o bloco !

Usando a segunda lei de Newton para esse bloco

Bem, vamos lá! Queremos saber qual a condição de para que o bloco não escorregue.

Nessa situação limite a força de atrito estático vai ter o seu valor máximo dado por

Como o bloco não se move na vertical podemos escrever que

assim

Então a aceleração máxima que o bloco pode ter sem escorregar é

Isolando

Show! Vamos para o nosso último bloco! Nesse caso temos normal com a mesa, peso e a tensão da corda.

Além disso, temos mais duas forças sobre o bloco ! São as reações das forças que o bloco exerce sobre o bloco , que são a normal e a força de atrito que desenhamos no passo anterior.

Como são reações, as forças em têm mesmo módulo, mas sentido oposto das forças em . Fica assim:

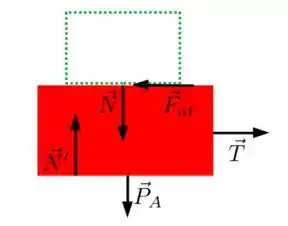
Na horizontal a segunda lei de Newton fica

Mas como já calculamos a e a aceleração do bloco tem que ser a mesma do bloco (por que os dois andam juntos)

Logo,

Show! Como já achamos a tensão agora só precisamos voltar para o bloco ! Para o bloco escrevemos que

Como o bloco está conectado com o bloco a acelereção é mesma que achamos antes

Igualando com a outra expressão para do passo anterior vamos ter que

Aí é só isolar !

Substituindo os valores numéricos

Show! Partiu pra próxima? :D