Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 4.Problemas - Ex. 47
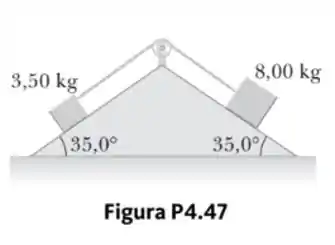
Dois blocos de massa e são conectados por um fio sem massa que passa sobre uma polia sem atrito (Fig. P4.47). Os planos inclinados são sem atrito. Encontre
- o módulo da aceleração de cada bloco e
- a tensão no fio.
Passo 1
E aiii galera, vamos fazer uma questão aqui?
Vem comigo!
Letra a:
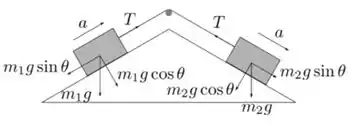
Para encontrar a, temos:
Para a primeira massa:
Para a segunda massa:
Então,
Passo 2
Letra b:
Agora, a partir da primeira equação, podemos escrever que a tensão é:
Resposta
Exercícios de Livros Relacionados
A Fig. 5-47 mostra dois blocos ligados por uma corda (de massa desprezível) que passa por uma polia sem atrito (também de massa desprezível). O conjunto é conhecido como máquina de Atwood. Um bloco te
Um homem de 85k g desce de uma altura de 10,0m em relação solo pendurado em uma corda que passa por uma roldana sem atrito e está presa na outra extremidade a um saco de areia de 65k g . Com que veloc
Na Fig. 5-46, três caixas são conectadas por cordas, uma das quais passa por uma polia de atrito e massa desprezíveis. As massas das caixas m a = 30,0k g , m b = 40,0k g , m c = 10,0k g . Quando o con
Na Figura P5.74, m 1 = 20,0k g e α = 53,1 ° . O coeficiente de atrito cinético entre o bloco de massa m 1 e o plano inclinado é μ C = 0,40 . Qual deverá ser a massa m 2 do bloco suspenso se ele tiver
Os blocos A , B e C são dispostos como indicado na Figura P 5.101 e ligados por cordas de massas desprezíveis. Os pesos de A e B são 25,0N cada, e o coeficiente de atrito cinético entre cada bloco e a