Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.Problemas - Ex. 87
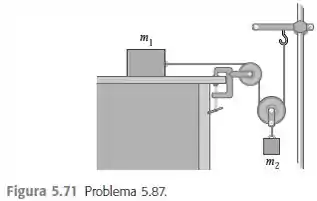
Determine a aceleração de cada bloco da Figura em função de , de e de . Não existe nenhum atrito em nenhuma parte do sistema.
Passo 1
Opa, tudo certinho aí? Espero que sim ^^.
Seguinte... temos o seguinte sistema:
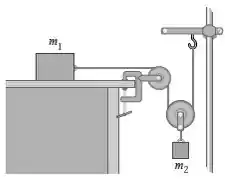
Queremos determinar a aceleração de cada bloco!!
Bem, vamos lá! Antes de tudo temos que escrever a segunda lei de Newton para os dois corpos, beleza?
Lembrando que essa Lei é dada assim:
Onde é a força resultante, é a massa e é a aceleração.
Passo 2
Para o bloco de massa a única força relevante é a tensão da corda (o peso e a normal se anulam), então a segunda lei de Newton fica:
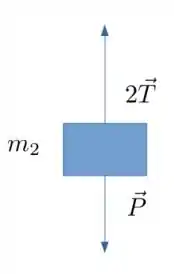
Para o bloco 2, temos o seu peso e a tensão. Mas como temos uma polia móvel a tensão nessa massa é ao invés de só
Passo 3
Agora vem um pulo do gato! Saca só! Vamos imaginar que o bloco 2 esteja descendo.
Só que, quando o bloco 1 anda uma distância para a direita, o bloco 2 cai uma altura . O que a polia móvel faz ali é fazer com que no bloco 2 tenha uma tensão (contrária ao movimento) que é o dobro do bloco 1, belezinha?
Se os dois têm o mesmo deslocamento podemos dizer que
Se derivarmos isso duas vezes dos dois lados da equação vamos ter a seguinte relação das acelerações
Passo 4
Com essa informação o nosso sistema de equações fica
Aí fechou! Vamos substituir a primeira na segunda
Agora é só jogar tudo que tem pra um lado e o que não tem para o outro
Passo 5
Agora é só partir para o abraço:
Como :
Show! Vamos pra próxima? :D