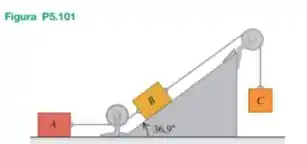
Os blocos , e são dispostos como indicado na Figura e ligados por cordas de massas desprezíveis. Os pesos de e são cada, e o coeficiente de atrito cinético entre cada bloco e a superfície é igual a . O bloco desce com velocidade constante. (a) Desenhe dois diagramas do corpo livre separados mostrando as forças que atuam sobre e sobre . (b) Ache a tensão na corda que liga os blocos e . (c) Qual é o peso do bloco ? (d) Se a corda que liga o bloco ao fosse cortada, qual seria a aceleração do bloco ?

A seguir segue o diagrama de forças que age sobre cada bloco:

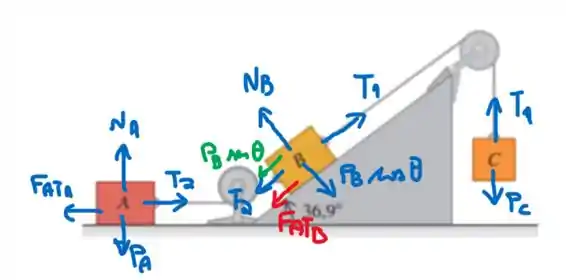
Como o bloco sobe, a força de atrito sobre ele aponta na direção descendente do plano inclinado. Note que eu já desenhei o peso decomposto. Observe também que temos duas trações diferentes no problema, já que são dois fios distintos. Como o bloco se move para direita, a força de atrito cinética sobre ele aponta para esquerda.

Como o sistema se move com velocidade constante, a força resultante sobre cada bloco deve ser nula:

Sabemos também que a força de atrito é dada por:

Como e , segue que:

As incógnitas são as tensões , e o peso .

No item (b) queremos achar :

Substituindo os valores:

Logo,

Usando a segunda equação, temos que

Logo,

Assim,

Da primeira equação do sistema, tiramos

Isso resolveu o item (c)!

Para terminar o problema, vamos ao item (c)! Rompendo o fio que liga e , podemos escrever as equações de movimento sem se preocupar com o bloco :

Vale ressaltar que agora vai assumir um novo valor.

Somando as equa�es, temos que:

Como já conhecemos os pesos de cada corpo, vamos escrever:

Assim,

Substituindo os valores e fazendo as contas, obtemos

Usando , temos

Valeu, galera! Até a próxima! 😉