Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 5.Problemas - Ex. 74

Na Figura P5.74, m 1 = 20,0   k g e α = 53,1 ° . O coeficiente de atrito cinético entre o bloco de massa m 1 e o plano inclinado é μ C = 0,40 . Qual deverá ser a massa m 2 do bloco suspenso se ele tiver que descer 12,0   m nos primeiros 3,00   s após o sistema ser liberado do repouso?

Passo 1

Fala pessoal, bora brincar mais um pouco de plano inclinado?

Nessa questão o primeiro passo é achar a aceleração do sistema via cinemática! Sabemos que a aceleração será constante, de modo que vale a equação do MUV:

Δ S = v 0 t + a t 2 2

Como v 0 = 0 , segue que

a = 2 Δ S t 2 = 2 ⋅ 12,0 3,00 2 → a = 2,67   m / s 2

Vamos guardar essa informação!

Passo 2

A seguir desenhamos as forças que agem em cada bloco:

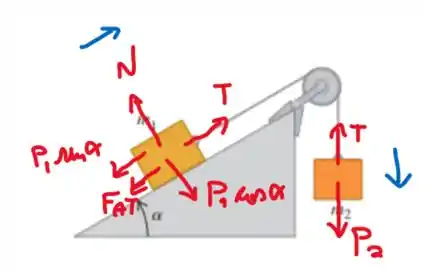
Já desenhei o peso do bloco 1 decomposto e considerei que o atrito aponta na direção descendente do plano inclinado, já que o bloco 1 deve subir enquanto o bloco 2 desce com aceleração a = 2,67   m / s 2 (achada no passo 1).

Olhando primeiro para o bloco 1, na direção perpendicular ao movimento devemos ter

N = P 1 cos ⁡ α = m 1 g cos ⁡ α

Já na direção do movimento temos

T - P 1   s e n   α - F a t = m 1   a

Usando F a t = μ C N , achamos

T - m 1 g   s e n   α - μ C m 1 g cos ⁡ α = m 1   a

Logo,

T - m 1 g s e n   α + μ C cos ⁡ α = m 1   a

Já para o bloco 2 temos

P 2 - T = m 2   a

Passo 3

Com isso, temos o sistema

T - m 1 g s e n   α + μ C cos ⁡ α = m 1   a m 2   g - T = m 2   a

Somando as equações, temos

m 2 g - m 1 g s e n   α + μ C cos ⁡ α = m 1 a + m 2 a

Vamos isolar m 2 :

m 2 g - a = m 1 a + m 1 g s e n   α + μ C cos ⁡ α

Logo,

m 2 = m 1 a + g s e n   α + μ C cos ⁡ α g - a

Agora é só substituir os valores:

m 2 = 20 ⋅ 2,67 + 9,8 ⋅ s e n   53,1 ° + 0,40 ⋅ cos ⁡ 53,1 ° 9,8 - 2,67

Fazendo as continhas:

m 2 = 36,1   k g

Resposta

m 2 = 36,1   k g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Inicialmente, o sistema dos corpos mostrados na Figura P4.51 é mantido sem movimento. A polia e todas as superfícies não têm atrito. Seja a força F → zero e assuma que m 1 pode se mover apenas vertica
Três corpos estão conectados sobre uma mesa, como mostrado na Figura P5.14. O coeficiente de atrito cinético entre o bloco de massa m 2 e a mesa é 0,350 . Os corpos têm massa de m 1=4,00k g , m 2= 1,0
O sistema mostrado na Figura P4.47 (Capítulo 4) tem uma aceleração de módulo 1,50m / s 2 . Suponha que o coeficiente de atrito cinético entre o bloco e o plano inclinado seja o mesmo para ambos os dec
Os sistemas mostrados na Figura P4.22 estão em equilíbrio. Se as balanças de mola estão calibradas em newtons, o que elas indicam? Ignore as massas das polias e cordas e considere que as polias e o pl
Considere os três corpos conectados, mostrados na Figura P5.43. Assuma primeiro que o plano inclinado não tem atrito e que o sistema está em equilíbrio. Em termos de m , g e θ , encontre a massa M eas