Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 28.8 - Ex. 39
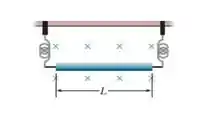
Um fio com de massa e de comprimento está suspenso por um par de contatos flexíveis na presença de um campo magnético uniforme de módulo (Fig. 28-40). Determine (a) o valor absoluto e (b) o sentido (para a direita ou para a esquerda) da corrente necessária para remover a tensão dos contatos.
Passo 1
E aí, galerinha!! 😉
Nesta situação temos um fio que está submerso em um campo magnético e está suspenso por contatos flexíveis:
Vamos aplicar aqui o conceito do equilíbrio das forças:
Mas quais forças atuam nesse camarada aí? Temos o peso apontando para baixo, e para encontrarmos o equilíbrio a força magnética deve apontar para cima.
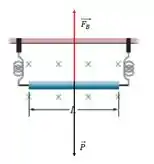
Legal? Vamos então partir para os cálculos dessas forças.
Passo 2
A força que o campo magnético exerce sobre o fio aponta para cima e tem um módulo igual à força gravitacional mg a que o fio está submetido.
Como o campo e a corrente são mutuamente perpendiculares, o módulo da força magnética é dado por , na qual é o comprimento do fio. Assim,
Logo podemos isolar a corrente por aqui:
com os valores de , , e , substituímos na equação e temos:
Tranquilo até aqui? 😬
Passo 3
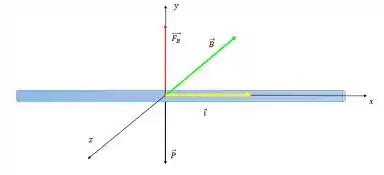
Para responder o item b. você pode usar a regra da mão direita, mas antes olha rapidinho a equação da força magnética em forma vetorial.
Pra fazer a regra da mão direita você tem que ir sempre no sentido da equação, mas como assim?
Tem que colocar a mão direita indo de para se fizer ao contrário o resultado não vai ser muito legal, entendeu? Então colocando a mão no sentido de para dentro da folha e abraçando o fio na direção da força o polegar vai apontar para a direita.
Resposta
(a)
(b) para a direita