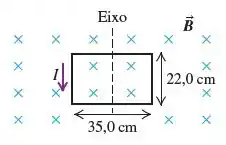
Uma bobina retangular de fio, com dimensões de 22,0 cm por 35,0 cm e que conduz uma corrente de 1,95 A, está orientada de modo que o plano de sua espira seja perpendicular a um campo magnético uniforme de 1,50 T, como indica a Figura. (a) Calcule a força resultante e o torque que o campo magnético exerce sobre a bobina. (b) A bobina é girada formando um ângulo de 30,0 ° em relação ao eixo indicado, com o lado esquerdo saindo do plano da figura e o lado direito entrando no plano. Calcule a força resultante e o torque que o campo magnético exerce agora sobre a bobina. (Dica: para ajudar a visualizar esse problema tridimensional, faça um desenho cuidadoso da bobina ao longo do eixo de rotação.)

letra a) τ = 0 , F R = 0 letra b) F R = 0 , τ = 112,6 ⋅ 10 - 3N m

Enunciado

letra a)

O torque é dado pela expressão:

Esse ângulo é o ângulo entre o campo magnético e a normal ao plano da espira.

Pelo desenho podemos perceber que o ângulo entre o plano da espira e o campo magnético é de .

Então

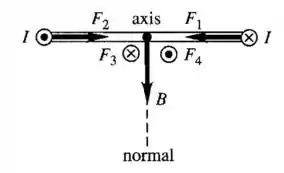
A força magnética depende do sentido da corrente e cada lado da espira terá uma força magnética.

Como a corrente tem sentidos opostos para cada lado da espira, a força magnética também terá.

Logo irão se anular.

letra b)

Vamos considerar agora que a bobina é girada formando um ângulo de em relação ao eixo indicado.

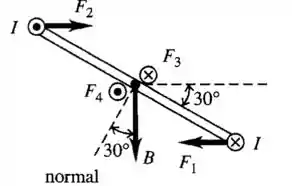
Podemos perceber que as forças de cada lado da espira ainda terão sentidos opostos. Logo:

A diferença entre o item anterior é que o ângulo entre o campo magnético e o plano da espirra será de .

Então:

O torque então será:

letra a),

letra b),