Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 27.1 - Ex. 94

Passo 1

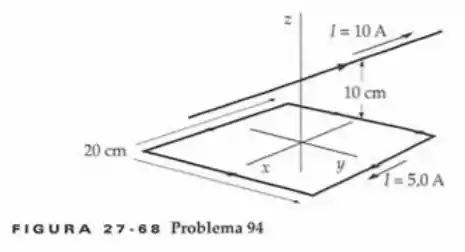
O campo B devido à corrente 10-A está no plano yz. A força líquida nos fios do quadrado em sua direção se cancelam e não contribuem a um torque líquido ou força. Podemos usar tau = l xx F , F = I l xx B , e a expressão para o campo magnético devido a um longo fio reto para expressar o torque atuando em cada dos fios e, portanto, o torque líquido atuando no anel.

Passo 2

Letra a:

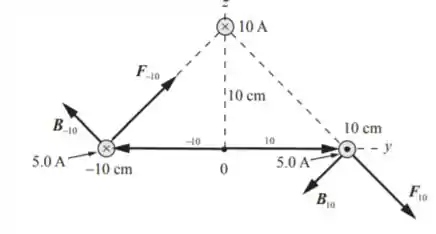
O torque líquido sobre o eixo x é a soma dos torques devido as forças F_10 e F_- 10 :

vec tau_l í q u i d o = vec tau_10 + vec tau_- 10 vec tau_l í q u i d o = vec l_10 xx vec F_10 + vec l_- 10 xx vec F_- 10

As forças serão:

vec F_10 = ( vec I l )_10 xx vec B_10 e vec F_- 10 = ( vec I vec l )_- 10 xx vec B_- 10

Substituindo:

vec tau_l í q u i d o = vec l_10 xx [( vec I vec l )_10 xx vec B_10] + vec l_- 10 xx [( vec I vec l )_- 10 xx vec B_- 10]

Os braços de alavanca para as forças atuantes nos fios em y = 10 cm e y = -10cm são:

vec e_10 = ( 0.10 m ) hat j a n d vec l_- 10 = - ( 0.10 m ) hat j

O campo magnético no fio em y = 10 cm é dado por:

vec B_10 = (mu_0)/(4 pi) (2 I)/(R) (1)/(sqrt(2)) ( - hat j - hat k ) o n d e R = sqrt(( 0.10 m )^2 + ( 0.10 m )^2) = 0.141 m

vec B_10 = (4 pi xx 10^(- 7) N // A^2)/(4 pi sqrt(2)) (2 ( 10 A ))/(0.141 m) ( - hat j - hat k ) = ( 10.0 mu T ) ( - hat j - hat k ) vec B_- 10 = ( 10.0 mu T ) ( - hat j + hat k )

Então, o torque:

vec tau_l í q u i d o = ( 0.10 m ) hat j xx [ ( 5.0 A ) ( 0.20 m ) hat i xx ( 10.0 mu T ) ( - hat j - hat k ) ] - ( 0.10 m ) hat j xx [ ( 5.0 A ) ( 0.20 m ) ( - hat i ) xx ( 10.0 mu T ) ( - hat j + hat k ) ] = - ( 2.0 mu N * m ) hat i

Passo 3

Letra b:

A rede de força atuando no circuito é a soma das forças agindo em seu quatro lados:

vec F_l í q u i d o = vec F_10 + vec F_- 10 vec F_10 = ( vec I underset(_)(l) )_10 xx vec B_10 = ( 5.0 A ) ( 0.20 m ) hat i xx ( 10.0 mu T ) ( - hat j - hat k ) = ( 10 mu N ) [ hat i xx ( - hat j - hat k ) ] = ( 10 mu N ) ( - hat k + hat j )

vec F_- 10 = ( vec I hat l )_- 10 xx vec B_- 10 = ( 5.0 A ) ( - 0.20 m ) hat i xx ( 10.0 mu T ) ( - hat j + hat k ) = ( - 10 mu N ) [ hat i xx ( - hat j + hat k ) ] = ( 10 mu N ) ( hat k + hat j )

Substitua F_10 e F_- 10 , na equação e simplifique para obter:

vec F_l í q u i d o = (10 mu N) (- hat k + hat j) + (10 mu N) (hat k + hat j) = ( 20 mu N ) hat j

Resposta

  1. vec tau_l í q u i d o = - ( 2.0 mu N * m ) hat i
  2. vec F_l í q u i d o = (10 mu N) (- hat k + hat j) + (10 mu N) (hat k + hat j) = ( 20 mu N ) hat j
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma espira retangular de 5,0 cm X 8,0 cm possui plano paralelo a um campo magnético de 0,19 T. A espira conduz uma corrente igual a 6,2 A. (a) Qual é o torque que atua sobre a espira? (b) Qual é o mód
Uma bobina retangular de fio, com dimensões de 22,0 cm por 35,0 cm e que conduz uma corrente de 1,95 A, está orientada de modo que o plano de sua espira seja perpendicular a um campo magnético uniform
Uma bobina com momento magnético 1,45A ⋅ m 2 está inicialmente orientada com seu momento magnético antiparalelo a um campo magnético com módulo igual a 0,835T . Qual é a variação da energia potencial
Momento magnético do átomo de hidrogênio. No modelo de Bohr do átomo de hidrogênio, no seu estado mais inferior de energia, o elétron órbita o próton a uma velocidade escalar de 2,2 × 10 6m / s em uma
Uma bobina retangular uniforme com massa total igual a 210 g e dimensões de 0,500 m 1,00 m está orientada no sentido perpendicular a um campo magnético uniforme de 3,00 T. Uma corrente de 2,0 A é repe