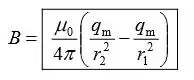Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 27.1 - Ex. 44

No Problema 43, uma expressão para a magnitude do campo magnético ao longo do eixo de um solenóide é fornecida. Para z >> l e l >> R, os ângulos θ1 e θ2 são muito pequenos, então as aproximações de pequeno ângulo c o s θ ≈ 1 - 1 2 θ 2 são altamente precisas. (a) Desenhe um diagrama e use-o para mostrar que, para essas condições, os ângulos podem ser aproximados como θ 1 ≈ R z + 1 2 e θ 2 ≈ R z - 1 2 l . (b) Usando essas aproximações, mostre que o campo magnético em pontos no eixo z onde z >> l pode ser escrito como B = μ 0 4 π   q n r 2 2 - q n r 1 2 , a quantidade q n é definida por q m = n I π R 2 .

Passo 1

Eae galera! Tudo tranquilo? Tendo uma visão geral da coisa, (a)vamos aplicar o pequeno ângulo em uma aproximação.

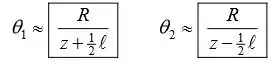
Passo 2

Vamo lá. (b) Expressar o campo magnético fora do solenóide:

Aplique a aproximação de pequeno ângulo para a função cosseno para obter:

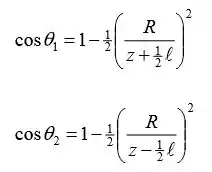
Substitua e simplifique para obter:

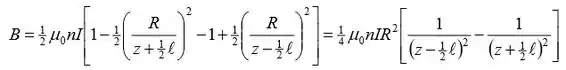
Passo 3

Obtendo:

Resposta

a ) θ 1 = R Z + 1 2 L ,     θ 2 = R Z - 1 2 L

b ) B = μ 0 4 π   q n r 2 2 - q n r 1 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A figura 29-78 mostra uma espira percorrida por uma corrente i = 2,00A . A espira é formada por uma semicircunferência de 4,00m de raio, dois quartos de circunferência de2,00m de raio cada um e três s
Na figura 29-71, um arranjo conhecido como bobina de Helmholtz é formado por duas bobinas coaxiais circulares de N espiras e raio R , separadas por uma distância s . As duas bobinas conduzem uma corre
Na figura 29-71, um arranjo conhecido como bobina de Helmholtz é formado por duas bobinas coaxiais circulares de N espiras e raio R , separadas por uma distância s . As duas bobinas conduzem uma corre
Uma espira quadrada de lado a conduz uma corrente i . Mostre que o módulo do campo magnético em um ponto de uma reta perpendicular ao plano da espira, passando pelo centro da espira é dado por B x = 4
Um motor cc possui um rotor e bobinas de campo ligados em série a uma resistência de 3,2Ω . Quando ele gira com sua carga total em uma linha de 120V , a fem do rotor é igual a 105V . (a) Qual é a corr