Uma bola de 20,0 kg é disparada da boca de um canhão com velocidade de 1000 m/s a um ângulo de 37,0 graus com a horizontal. Uma segunda bola é disparada a um ângulo de 90,0 graus. Use o modelo de sistema isolado para encontrar (a) a altura máxima alcançada por cada bola e (b) a energia mecânica total do sistema bola-Terra na altura máxima de cada bola. Estabeleça y = 0 no canhão.
Passo 1
(a)Aqui, pra descobrir a altura máxima de cada bola, a gente precisa começar calculando a velocidade que elas vão ter na componente vertical.
A gente calcula isso seguindo esse esqueminha, já muito usado ao longo desse livro:
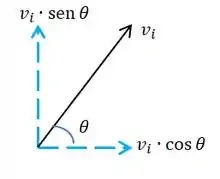
Então, gente, se a velocidade original da bola lançada a é , a velocidade dela na vertical vai valer:
Bom, essa é a velocidade que a bola tem no percurso vertical, e como ela tem essa velocidade no início do percurso, ela tem a energia cinética máxima nesse mesmo momento.
Quando ela chegar na altura máxima que ela pode alcançar, toda energia cinética vai virar energia potencial gravitacional!
Ou seja, pela conservação de energia, a gente vai ter:
Aplicando as formulinhas:
Considerando , aplicamos nossos dados e vamos ter:
Agora a gente faz o mesmo pra outra bola, só que como ela já é lançada a com a horizontal, então a velocidade dela na vertical é exatamente a velocidade original dela, .
Com isso, a gente faz a mesma continha, determinando agora. A gente vai ter:
Simplificamos:
E aplicamos os nossos dados:
Passo 2
(b)A energia mecânica, como a gente sabe, é a energia total do sistema.
No caso, a gente precisa calcular ela pelas energias potenciais de cada bola na altura máxima alcançada, como pedido no enunciado.
Pelas energias potenciais, a gente vai ter:
Resposta
(a)
(b)