Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 6.Exercícios e Problemas - Ex. 20
6.20P A esfera vista na Figura 6.17 está suspensa por um elástico de massa nula e constante elástica . A esfera é solta do repouso quando o elástico está com seu comprimento de equilíbrio (sem tensão) . A) Descreva o movimento do sistema. B) Quais são os pontos de retorno da oscilação?
Passo 1
Tranquilovski galerinha, a figura 6.17 é dada pra gente como:
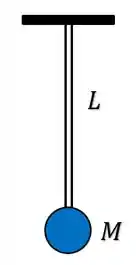
Quando a esfera de massa é liberada, a força peso que ela possui vai começar a realizar um trabalho durante a queda, só que a energia que esse trabalho realiza não é perdida durante a queda, ela é trasnferida para o elástico até que ele se estique uma distância máxima:
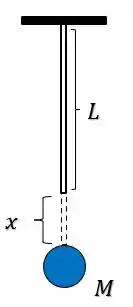
Nesse ponto, toda a energia do trabalho que a força peso realizou foi trasnferida para o elástico, e a força contrária ao movimento que o elástico exerce sobre a esfera já superou a força peso da prórpia esfera. Dessa forma a esfera volta a subir, transferindo parcialmente a energia armazenada no elástico de volta pra esfera.
Passo 2
Iradoso, isso quer dizer que de acordo com a conservação da energia mecânica, a energia inicial vai ser igual a energia final:
Para a energia mecânica inicial, temos apenas a presença de energia potencial gravitacional, devido à queda de metros a altura inicial será tal que:
Já no ponto mais baixo, a energia mecânica final será formada apenas pela energia potencial elástica do elástico, onde a variação do tamanho do elástico é exatamente :
Então se a gente igualar as energias teremos que:
Logo:
Portanto, a esfera inverte seu movimento quando atinge um ponto tal que: