Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 18.Problemas - Ex. 38

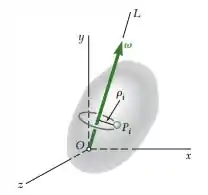
Mostre que a energia cinética de um corpo rígido com um ponto fixo O pode ser expressa por T = 1 2 I O L ω → 2 , onde ω → é a velocidade angular instantânea do corpo e I O L é seu momento de inércia em relação à linha de ação OL de ω → . Deduza essa expressão (a) a partir das Eqs. (9.46) e (18.19), (b) considerando T como a soma das energias cinéticas de partículas P i que descrevem círculos de raios ρ i em torno da linha OL.

Passo 1

Vamos lá resolver mais essa. A energia cinética de um corpo rígido é dada por:

T = 1 2 I x ω x 2 + I y ω y 2 + I z ω z 2 - 2 I x y ω x ω y - 2 I y z ω y ω z - 2 I x z ω x ω z

Vamos assumir que, para o corpo:

ω x = ω cos ⁡ θ x = ω λ x

ω y = ω cos ⁡ θ y = ω λ y

ω z = ω cos ⁡ θ z = ω λ _ z

Passo 2

Substituindo as expressões para as velocidades angulares na expressão para a energia cinética:

T = 1 2 I x λ x 2 ω 2 + I y λ y 2 ω 2 + I z λ z 2 ω 2 - 2 I x y λ x λ y ω 2 - 2 I y z λ y λ z ω 2 - 2 I x z λ x λ z ω 2

T = 1 2 I x λ x 2 + I y λ y 2 + I z λ z 2 - 2 I x y λ x λ y - 2 I y z λ y λ z - 2 I x z λ x λ z ω 2  

T = 1 2 I O L ω 2

Passo 3

Como cada partícula de massa Δ m i tem uma trajetória circular de raio ρ i , a velocidade da partícula é dada por v i = ρ i ω . Assim, a energia cinética da partícula é dada por:

Δ T i = 1 2 Δ m i v i 2 = 1 2 Δ m i ρ i 2 ω 2

A energia cinética do corpo é:

T = ∑ Δ T i = 1 2 ∑ Δ m i ρ i 2 ω 2

Como I O L = ∑ Δ m i ρ i 2 , logo

T = 1 2 I O L ω 2

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O topo mostrado é suportado no Ponto fixo 0 e seus momentos de inércia em torno de seu eixo de simetria e em torno de um eixo transversal em 0 são denotados, respectivamente, por I e I ' . (a) Mostre
Uma esfera sólida de raio c = 3 pol. É anexada como mostrado ao cabo AB. Observa-se que a esfera processa a uma taxa constante ϕ ˙ = 6 r a d / s em torno do eixo vertical AD. Sabendo que β = 40 ∘ , de
Um cubo sólido do lado c = 80 mm é preso como mostrado ao cabo AB. Observa-se que gira a uma taxa ψ ˙ = 40 r a d / s em torno de sua diagonal BC e precessa a uma taxa constante ϕ ˙ = 5 r a d / s em to
Um satélite de 2500 kg tem 2,4 de altura e bases octogonais com lados de 1,2 m. Os eixos de coordenadas mostrados são os principais eixos centróides de inércia do satélite, e seus raios de giração são
Mostre que o vetor de velocidade angular w de um corpo axissimétrico sob nenhuma força é observado a partir do próprio corpo girando em torno do eixo de simetria a uma taxa constante n = I ' - I I ' ω