Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 6.Exercícios e Problemas - Ex. 21
6.21P* Refaça o Problema 6.16 supondo que o elástico tenha uma massa .
Passo 1
Belezoca de motoca, no exercício anterior nossa figura era:
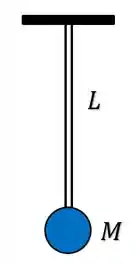
Só que como agora temos que o elástico também tem uma massa , vamos representar nessa figura o centro de massa do elástico, onde a massa está concentrada:
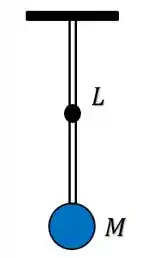
Quando a esfera de massa é liberada, a esfera vai entrar em queda até atingir uma distância :
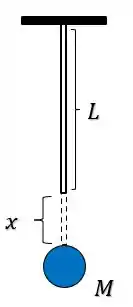
Só que quando isso acontece, o centro de massa do elástico também se move (já que o elástico se estica), e como ele divide o elástico em dois, e o elástico inteiro percorre um distância em um sentido, o centro de massa vai percorrer metade dessa distância no mesmo sentido, tal que nesse ponto teremos:
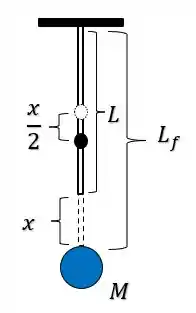
Passo 2
Xuxu no mel, isso quer dizer que se a gente aplicar a conservação da energia aqui, vamos ter que levar em conta que no momento inicial, tanto a esfera, quanto o elástico vão possuir energia potencial gravitacional:
Como a esfera cai por uma distância , temos que:
Já o centro de massa do elástico está caindo por uma distância , tal que sua energia potencial gravitacional é:
Dessa forma a energia mecânica inicial total é:
Já a energia mecânica final, dada no ponto mais baixo do movimento, vai ser constituída apenas de energia potencial elástica devido a sua deformação de metros:
Então igualando as energias inicial e final, de acordo com a conservação da energia, temos:
Isolando , temos:
Logo:
Portanto, o ponto de inversão do movimento é dado por :
