Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 8.1 - Ex. 50

Uma laranja esférica de 0,34   k g de massa e 2,0   c m de raio é largada do topo de um edifício de 35   m de altura. Após atingir o solo, o formato da laranja é de uma panqueca de 0,50   c m de espessura. Despreze a resistência do ar e considere a colisão completamente inelástica.

(a) Quanto tempo a laranja levou para ser esmagada e atingir o repouso?

(b) Qual foi a força média exercida pelo chão sobre a laranja durante a colisão?

Passo 1

A figura abaixo representa a laranja se movendo com velocidade v , logo antes do impacto, depois de cair da atura de 35   m . Considere o sistema consituído apenas pela laranja e o zero da energia potencial gravitacional sendo o centro de massa da laranja esmagada. As forças externas são a força gravitacional ( F → g ) que age durante a queda da laranja e a força normal ( F → N ) exercida pelo chão qunado a laranja é esmagada. Podemos achar o tempo de esmagamento pelo deslocamento do centro de massa da laranja quando ela para e sua velocidade média ( v → m ) durante esse perído assumindo aceleração constante. Também podemos usar o teorema do Impulso e Variação da Quantidade de Movimento para achar a força média ( F → m ) exercida pelo chão na laranja em sua desaceleração.

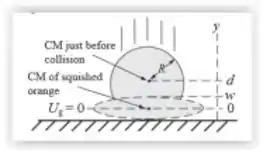
Passo 2

(a) Expressando o tempo de parada ∆ t da laranja em função da sua velocidade média e da distância d percorrida pelo seu centro de massa:

∆ t =   d v m =   R - 1 2 w v m   ( I )

Onde w é a espessura da laranja esmagada.

Para achar v m , aplicaremos a conservação de energia mecânica:

∆ K + ∆ U = 0

Porém, como sabemos que ela foi largada do topo do edifício, K i =   0

K f +   U g , f -   U f , i = 0

Substituindo as variáveis:

1 2 m v 2 + m g d - m g h - d = 0

Isolando v e sabendo que d ≪ h , ficamos com:

1 2 m v 2 - m g h = 0

v   ≈   2 g h   ( I I )

Como assumimos aceleração constante para a laranja sendo esmagada, temos que

v m =   1 2 v =   1 2 2 g h

Trocando v m na equação ( I ) e simplificando:

∆ t =   R - 1 2 w 1 2 2 g h

∆ t =   2 R - 1 2 w 2 g h

∆ t =   2 0,02   m - 1 2 ( 0,5   m ) 2 ( 9,81   m / s 2 ( 35   m ) = 1,336 ×   10 - 3   s

∆ t ≅ 1,3   m s

Passo 3

(b) Aplicando o Teorema do Impulso e Variação da quantidade de Movimento para a laranja sendo esmagada:

F → m ∆ t =   ∆ p → =   p → f -   p → i

Mas como v f   =   0 , p f   =   0 :

F m ∆ t   =   p i

F m   =   m v i ∆ t   ( I I I )

Passo 4

Substituímos a equação ( I I ) na equação I I I , pois sabemos que v i = v :

F m   =   m v i ∆ t

F m   =   m 2 g h ∆ t

E, por último colocando os valores numéricos nas variáveis, obtemos que:

F m   =   ( 0,34   k g ) 2 ( 9,81 m / s 2   ) ( 35   m ) ( 1,336 ×   10 - 3   s )

F m ≈ 6,7   k N

Resposta

(a) ∆ t ≅ 1,3   m s  

(b) F m ≈ 6,7   k N  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O motor de um sistema de manobra orbital em um ônibus espacial exerce uma força igual a 26700N j ^ durante 3,90s , ejetando uma quantidade de massa de combustível desprezível em relação à massa de 950
No instante t = 0 , um foguete de 2150k g no espaço sideral aciona um motor que exerce uma força crescente sobre ele no sentido positivo dex . Essa força obedece à equação F x = A t 2 , ondet é o inte
Uma pedra de 2,0k g está deslizando a 5,0m / s da esquerda para a direita sobre uma superfície horizontal sem atrito, quando é repentinamente atingida por um objeto que exerce uma grande força horizon
No Exemplo Conceitual 8.1 (Seção 8.1), mostre que o barco de massa 2 m possui, ao chegar na linha final, um momento linear 2 vezes maior do que o momento linear do barco de massa m .
Dois veículos se aproximam de um cruzamento. Um deles é uma caminhonete de 2500k g que se desloca a 14,0m / s do leste para oeste (no sentido negativo de x ), e o outro é um carro de passeio de 1500k