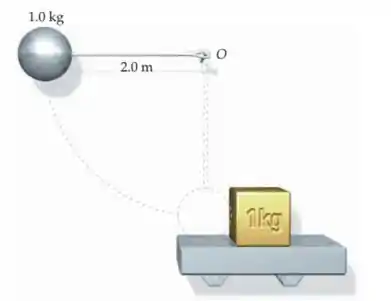
Uma bola de aço de e uma corda de e massa desprezível formam um pêndulo simples que pode pivotear sem atrito em torno do ponto O, como na figura. Este pêndulo é largado do repouso a partir de uma posição horizontal e, quando a bola está em sua posição mais baixa, ela colide com um bloco de que está em repouso sobre uma prateleira. Suponha a colisão perfeitamente elástica e que o coeficiente de atrito cinético entre o bloco e a prateleira vale . (a) Qual é a velocidade do bloco logo após o impacto? (b) Até que distância o bloco escorrega antes de parar (supondo a prateleira suficientemente longa)?

a) Conservação da energia da bola entre o ponto mais alto e o ponto mais baixo:

Conservação da quantidade de movimento no choque, supondo que a bola vai voltar para trás e o bloco vai para a frente (para que a velocidade de afastamento seja a soma das velocidades):

Coeficiente de restituição para o choque (colisão elástica significa ):

Juntando as equações e : e , ou seja, a bola para e bloco segue com a velocidade original da bola.

b) Para determinar a distância que ele vai percorrer, vamos usar a equação de Torricelli:

Queremos que ele pare, e portanto .

A força resultante no eixo x é:

Logo,

Substituindo os valores: