Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 7.1 - Ex. 5
Uma bola de beisebol é lançada do telhado de um edifício de 22,0 m de altura com uma velocidade inicial de 12,0 m/s e dirigida formando um ângulo de 53,1º acima da horizontal.
a) Qual é a velocidade da bola imediatamente antes de colidir com o solo? Use o método da energia e despreze a resistência do ar.
b) Qual seria a resposta da parte (a) se a velocidade inicial formasse um ângulo de 53,1° abaixo da horizontal?
c) Se você não desprezar a resistência do ar, a maior velocidade será obtida na parte
(a) ou na parte (b)?
Passo 1
Opa, bora lá!
O enunciado fala de uma bola de beisebol que é lançada do telhado de um edifício de de altura com uma velocidade inicial de formando um ângulo de acima da horizontal.
Vamos desenhar um esqueminha:
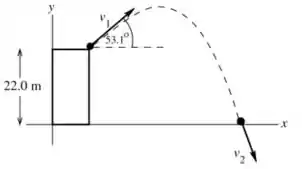
Vamos usar a equação de balanço de energia:
Resolveremos por para obtermos a velocidade. É importante lembrar que W = 0 pois a única força na bola enquanto está no ar é gravidade.
Temos que:
Substituindo as equações temos:
Como , então:
Passo 2
Agora a gente tem que responder a mesma pergunta, mas a velocidade inicial forma ângulo de abaixo da horizontal!
Nesse caso nada mudaria no cálculo. A expressão derivada na parte (a) para é independente do ângulo, então também!
Passo 3
Para o item (c), é possível verificar que a bola percorre uma distância menor na parte (b), portanto, nesse caso, a resistência do ar terá menos efeito.
Resposta
a)
b) também, pois independe do ângulo.
c) caso (b), pois a resistência do ar terá menos efeito.