Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 3.Problemas - Ex. 76
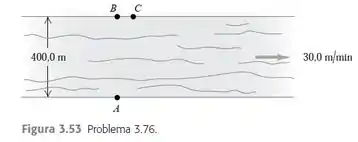
Um rio com largura de 400,0 m corre de oeste para leste a 30,0 m/min. Seu barco se move a 100,0 m/min em relação à água, não importando a direção em que segue. Para atravessar esse rio, você parte de um embarcadouro no ponto A localizado na margem sul. Há um barco aportando na direção exatamente oposta, no ponto B localizado na margem norte, e ainda outro no ponto C, 75,0 m abaixo de B (Figura 3.53). a) Aonde na margem norte você aportará, se orientar seu barco perpendicularmente à correnteza e qual distância terá percorrido? b) Se você inicialmente orientar seu barco diretamente para o ponto C e não mudaressa posição em relação à margem, onde na margem norte você aportará? c) Para chegar ao ponto C: i) para qual posição você deve orientar o barco, ii) quanto tempo levará para atravessar o rio, iii) qual distância percorrerá e iv) qual a velocidade escalar do seu barco, conforme medido por um observador parado na margem do rio?
Passo 1
Fala aí!
Temos a seguinte situação:
Todas as velocidades são constantes, portanto a distância percorrida é:
Quando é a magnitude da velocidade do barco em relação à terra.
As velocidades relativas são:
E são relacionadas por:
Seja ao leste e ao norte.
Sabemos que:
E que:
A direção de é a direção na qual o barco está apontado.
Bora lá!
Passo 2
- Como e .
- está direcionado pelo ângulo leste do norte, onde:
- Então, para chegar ao ponto C:
Então,
E
O momento de atravessar o rio é dado por:
E
Você aterrissará a leste do ponto B, que fica a a leste do ponto C. A distância que você percorreu é dada por:
Show?
Passo 3
E então:
Tranquilo até aqui?
Passo 4
E então, temos que:
E
E agora podemos calcular:
E
E para calcular o tempo que isso ocorre:
Assim,
Você pousará rio abaixo de B, então a rio abaixo de C.
Bacana, não é?
Passo 5
- Se você chegar ao ponto C, então está direcionado a leste do norte, que é norte do leste. Não sabemos a magnitude de e a direção de .
- O tempo para atravessar o rio é:
- Você viaja de A a C, a uma distância de:
- E a velocidade escalar do seu barco, conforme medido por um observador parado na margem do rio é:
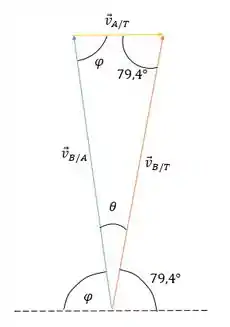
Na parte (a), descobrimos que, se apontarmos o barco para o norte, pousaremos a leste de C, para pousar em C, devemos apontar o barco para oeste do norte. Vamos fazer estar em um ângulo do norte do oeste. Vejamos no diagrama de adição de velocidaderelatva acima. A lei dos senos nos diz que:
Isso implica que:
E então,
E isso implica que:
O barco vai seguir norte de oeste, então oeste de norte.
Assim,
E
Observe que esses dois componentes fornecem a direção de a ao norte de leste, conforme necessário.
Estamos quase lá!
Passo 6
Bora continuar!
Passo 7
Legal?
Passo 8
Observe que , a distância percorrida (além de uma pequena diferença devido ao arredondamento).
E fim! O que achou? Responde Aí!
Resposta
- Você aterrissará a leste do ponto B, que fica a a leste do ponto C. A distância que você percorreu é ;
- Você pousará rio abaixo de B, então a rio abaixo de C;