Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 8.4 - Ex. 43
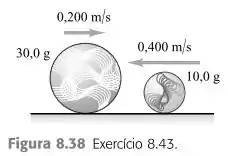
Uma bola de gude de desloca-se com velocidade de da direita para a esquerda sobre uma pista horizontal sem atrito e colide frontalmente com outra bola de gude de que se desloca com velocidade de da esquerda para a direita (Figura 8.38).
a) Determine o módulo, a direção e o sentido de cada bola de gude depois da colisão. (Como a colisão é frontal, todos os movimentos ocorrem ao longo da mesma linha reta.)
b) Calcule a variação do momento linear (isto é, o momento linear depois da colisão menos o momento linear antes da colisão) para cada bola de gude. Compare os valores obtidos para cada bola de gude.
c) Calcule a variação de energia cinética (isto é, a energia cinética depois da colisão menos a energia cinética antes da colisão) para cada bola de gude. Compare os valores obtidos para cada bola de gude.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente encontrar (a) o módulo, a direção e o sentido de cada bola de gude depois da colisão, (b) a variação do momento linear para cada bola de gude e (c) a variação de energia cinética para cada uma.
Pra isso, vamos considerar o princípio de conservação do momento linear e calcular a velocidade de cada bola depois da colisão. Em seguida, vamos calcular a variação do momento linear, que é o momento linear depois da colisão menos o momento linear antes da colisão. Por fim, vamos fazer a energia cinética depois da colisão menos a energia cinética antes da colisão para obter a variação de energia cinética .
Vamos lá!
Passo 2
a) Dado que a colisão acontece somente em um eixo, que é o , para descobrirmos a velocidade das bolinhas após a colisão, basta que utilizemos a lei de conservação do momento linear, uma vez que é uma lei que relaciona as massas das bolinhas com suas velocidades, que é o que queremos descobrir. Assim, temos que:
E como , então teremos o seguinte:
No qual os termos significam:
massa da segunda bolinha;
massa da primeira bolinha;
velocidade inicial da segunda bolinha;
velocidade inicial da primeira bolinha.
velocidade final da primeira bolinha;
velocidade final da segunda bolinha.
Se substituirmos os valores nas incógnitas, teremos:
Como temos duas incógnitas, então agora temos o dever de encontrar outra expressão com essas duas mesmas incógnitas para que, assim, possamos determinar seus valores utilizando um sistema de equações ou algo do tipo, ok?
Passo 3
Do capítulo do Young, temos que quando há uma colisão retilínea e elástica entre dois corpos, a velocidade relativa antes da colisão é igual e contrária à velocidade relativa depois da colisão. Sendo assim, temos que:
Substituindo os valores, teremos:
Que nos leva ao sistema de equações:
Passo 4
Resolvendo o sistema acima, teremos os seguintes valores para e :
O sentido da primeira bola de gude é para a esquerda, o que explica o sinal de negativo no valor de sua velocidade. Já o sentido da segunda bola de gude é para a direita.
Passo 5
b) Para a primeira bolinha de gude, temos o seguinte:
Substituindo os valores, temos:
Para a segunda bolinha de gude, temos o seguinte:
Substituindo os valores, temos:
Os valores nos levam a conluir que a variação de momento linear para ambos é a mesma. No entanto, o que difere é apenas o sentido em que seguem após a colisão.
Passo 6
c) Agora considerando a energia cinética de cada uma, para a primeira bolinha de gude, temos o seguinte:
Substituindo os valores, teremos:
Para a segunda bolinha de gude, temos o seguinte:
Substituindo os valores, teremos:
Assim como na letra anterior, os resultados nos levam a concluir que, em módulo, as bolinhas apresentaram exatamente a mesma quantidade de variação de energia cinética.
Valeu, galera! Até a próxima! 😉
Resposta
a)
b)
c)