Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 7.Problemas - Ex. 83
Um instrumento cortante controlado por um microprocessador possui diversas forças atuando sobre ele. Uma das forças é dada por uma força orientada no sentido negativo do eixo Oy cujo módulo depende da posição do instrumento. O valor da constante é dado por .
Considere o deslocamento do instrumento desde a origem até o ponto , .
a) Calcule o trabalho realizado pela força sobre o instrumento para um deslocamento ao longo da reta que conecta esses dois pontos.
b) Calcule o trabalho realizado pela força sobre o instrumento quando ele é inicialmente deslocado ao longo do eixo Ox até o ponto , e a seguir deslocado paralelamente ao eixo Oy até o ponto , y.
c) Compare os resultados dos trabalhos realizados por nessas duas trajetórias. A força é conservativa ou não conservativa? Justifique sua resposta.
Passo 1
Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
Temos aqui um instrumento sujeito a diversas forças, iremos analisar aqui a força que está em direção negativa no eixo .
Aqui iremos analisar o trabalho da força até por diferentes caminhos.
Passo 2
- Oi, galerinha! Belezinha? Se liga, lembra que trabalho é força vezes deslocamento? Mas aqui a força não é constante, para calcular usamos a integral,
- Respondendo o item (b), para o deslocamento do ponto 1 ao ponto 2,
E como a força varia de acordo com apenas uma coordenada, avaliaremos ao longo do caminho. O esquema é indicado abaixo
Fazemos então
Igualando,
No caminho, , então
Substituindo na integral, temos
Passo 2
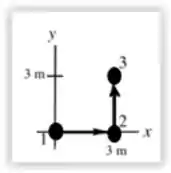
Então,
e
pois a força é perpendicular a o deslocamento em cada ponto ao longo do caminho.
Para o deslocamento do ponto 2 para o ponto 3,
Substituindo
Integrando, temos
Para esses dois caminhos entre os mesmos pontos inicial e final, o trabalho é diferente; portanto, a força não é conservadora.
Resposta
a)
b)
c) a força não é conservadora.