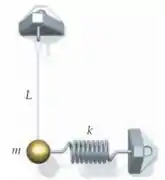
A bolinha de um pêndulo de massa está presa a uma mola leve de comprimento e também está presa a uma mola com constante de força . Com o pêndulo na posição mostrada na figura, a mola está no seu comprimento não-comprimido. Se a bolinha é puxada para o lado de forma que a corda faça um pequeno ângulo com a vertical e solta, qual é a rapidez do pêndulo conforme ele passa pela posição de equilíbrio? Dica: Lembre das aproximações para ângulos pequenos: se é expresso em radianos, e se , então e .

Quando você puxa o pêndulo para o lado você dá energia potencial gravitacional a ele (porque ele ganha altura) e dá energia potencial elástica para a mola (porque ela é comprimida). Vamos encontrar expressões para essas duas energias:

E a altura que o pêndulo ganha quando é deslocado por um ângulo é:

E a energia potencial elástica é um pouco mais complicada, considerando que o pêndulo não se move exatamente em linha reta. Mas como o ângulo é pequeno, podemos aproximar o arco de círculo por um segmento de reta, então:

E quando a bolinha passa pelo ponto de equilíbrio, essas duas energias terão sido convertidas inteiramente em metros: