Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 6.Exercícios e Problemas - Ex. 05
Em cada um dos dois diagramas de corpo livre, as forças são exercidas sobre um objeto de 2,0 kg. Para cada diagrama, determine os valores de e , os componentes e da aceleração.
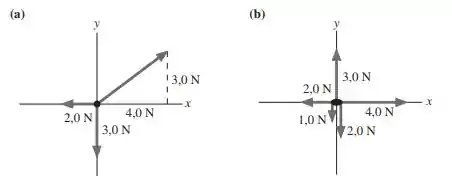
Passo 1
Cada aceleração e poderá ser calculada a partir da segunda lei de Newton:
Portanto, devemos decompor as forças nas direções e e calcular a força resultante.
Passo 2
- Do diagrama, temos:
- Procedemos da mesma forma:
(note que a força para a esquerda possui sinal negativo).
ou seja, a partícula está em equilíbrio no eixo y.
Passo 3
Resposta
- e .
- e .
Exercícios de Livros Relacionados
Uma força imprime a um objeto de massa m 1 uma aceleração de 12,0m / s ² ² e a um objeto de massa m 2 uma aceleração de 3,30m / s ² ² . Que aceleração essa mesma força imprimiria a um objeto de massa
Qual é o módulo da força necessária para imprimir uma aceleração de 1,4 m / s 2 em uma geladeira com massa 135 k g ?
Se uma força resultante horizontal de 132 N é aplicada a uma pessoa com massa de 60 k g em repouso na beira de uma piscina, qual é a aceleração produzida?
Um portuário aplica uma força horizontal constante de 80 N a um bloco de gelo sobre uma superfície horizontal lisa. A força de atrito é desprezível. O bloco parte do repouso e se move 11 m em 5 s . a
Uma caixa está em repouso sobre um lago congelado, que é uma superfície horizontal sem atrito. Se um pescador aplica uma força horizontal de módulo 48 N sobre a caixa, produzindo uma aceleração de 2,2