Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 2.1 - Ex. 16
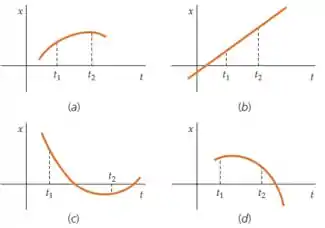
Para cada um dos quatro gráficos de -versus- na figura abaixo, responda as seguintes perguntas. (a) A velocidade em é maior, menor ou igual à velocidade em ? (b) A rapidez em é maior, menor ou igual à rapidez em ?
Passo 1
(a) Nesses gráficos de -, a velocidade é a inclinação do gráfico. Vamos dar o exemplo em um dos gráficos, e então seguir a mesma lógica para os outros.
No gráfico , vamos desenhar as retas tangentes nos pontos e :
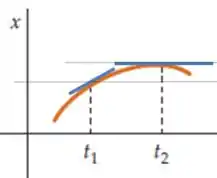
Claramente a reta tangente em é mais inclinada em relação à horizontal, além de que a inclinação em é (possivelmente) negativa, então:
No gráfico a inclinação é constante, então:
No gráfico a inclinação em é claramente negativa, então:
E no gráfico a inclinação em é negativa:
Passo 2
(b) Agora nós vamos considerar a rapidez, ao invés da velocidade. Nesse casos pegamos o módulo das inclinações, desconsiderando o sinal.
Vamos usar para representar a rapidez, assim evitamos confusão com a velocidade.
No gráfico , a inclinação de é bem próxima de zero:
No gráfico as inclinações continuam iguais, então:
No gráfico , a inclinação em é muito mais acentuada do que em , apesar de ser negativa. Como estamos considerando o módulo das inclinações:
E no gráfico , a inclinação em também é mais acentuada, o que implica em uma velocidade negativa, mas uma rapidez muito alta:
Resposta
(a) Em , ; Em , ; Em c ; Em .
(b) Em , ; Em , ; Em ; Em .