Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 2.1 - Ex. 15

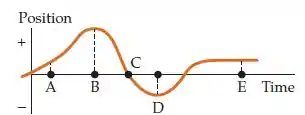
Um objeto se move ao longo de uma linha reta. Seu gráfico de posição-versus-tempo é mostrado na figura abaixo. Em qual tempo, ou tempos (a) a sua rapidez está em um mínimo, (b) a sua aceleração é positiva e (c) a sua velocidade é negativa.

Passo 1

(a) A rapidez do objeto é o módulo da inclinação do gráfico do enunciado. É importante lembrar desse “módulo”, porque do contrário teríamos que lembrar de comparar os sinais das inclinações.

Então os pontos de mínimo da rapidez são aqueles em que ela é nula, ou seja, que a inclinação do gráfico é nula. Isso acontece nos pontos B , D e E .

Passo 2

(b) A aceleração é positiva nos instantes em que a derivada segunda é positiva. Isso quer dizer que a inclinação do gráfico está aumentando.

Isso acontece apenas nos pontos A e D .

Passo 3

(c) A velocidade é negativa nos instantes em que a inclinação do gráfico é negativa, ou seja, a função é decrescente.

Isso acontece apenas no ponto C .

Resposta

(a) Pontos B , D e E . (b) Pontos A e D . (c) Ponto C .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A figura abaixo mostra nove gráficos de posição, velocidade e aceleração para objetos se movendo ao longo de uma linha reta. Indique os gráficos que atendem às seguintes condições: (a) velocidade é co
Um carro viajando com velocidade constante passa pela origem no tempo t = 0 . Nesse instante, um caminhão, em repouso na origem, começa a acelerar uniformemente a partir do repouso. A figura 2-34 most
Qual(is) gráfico(s) (ou nenhum deles) de v x em função de t na figura abaixo melhor descreve o movimento de uma partícula com (a) velocidade positiva e rapidez crescente, (b) velocidade positiva e ace
Qual(is) gráficos(s) (ou nenhum deles), de v x em função de t na figura abaixo melhor descreve o movimento de uma partícula com (a) velocidade negativa e rapidez crescente, (b) velocidade negativa e a
As posições de dois carros em pistas paralelas de um trecho reto de estrada estão plotadas como funções do tempo na figura abaixo. Tome os valores positivos de x como estando à direita da origem. Resp