Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 2.Exercícios e Problemas - Ex. 25

A posição de uma partícula sobre o eixo x é dada pela função x = ( t 2 - 4 t + 2 )   m , onde t   está em s .

a. Trace um gráfico da posição versus tempo para o intervalo 0   s ≤ t ≤   5   s . Faça isso calculando e marcando x a cada 0,5   s , desde 0 até 5 s, e depois trace uma curva suave ligando os pontos obtidos.

b. Calculando o valor da derivada no instante, determine a velocidade da partícula neste instante. Compare o resultado com o que você obteve no item anterior.

c. Existe algum ponto de retorno no movimento da partícula? Em caso positivo, em que posição ou posições?

d. Onde se encontra a partícula em t =   4,0   m / s ?

e. Trace um diagrama de movimento para a partícula.

Passo 1

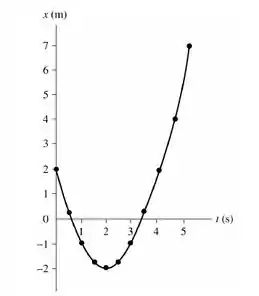
  1. Bom galerinha, com as intrunções dada o nosso gráfico fica da seguinte maneira:

    2. Passo 2

  2. E então, calculando a derivada, temos que:

    3. d x d t = v x = 2 t - 4

    ⇒ v x e m t = 1 s = 2 m s 2 1 s - 4 m s = - 2 m s

    Passo 3

  3. Há um ponto de inflexão em t = 2   s .

    4. Passo 4

  4. Usando a equação da parte (b):

    5. v x = 4   m / s = 2 t - 4 m / s  

    ⇒ t = 4

    Uma vez que

    x = t 2 - 4 t + 2 m ,

    x = 2 m

    Passo 5

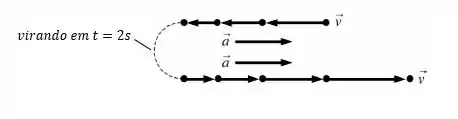
  5. Assim, o nosso diagrama fica da seguinte forma:

Resposta

  2. v x = - 2 m s
  3. em t = 2   s
  4. x = 2 m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Qual das curvas de posição em função do tempo na figura abaixo melhor representam o movimento de um objeto (a) com aceleração positiva, (b) com velocidade constante positiva, (c) que está sempre em re
O diagrama na figura abaixo mostra a localização de um objeto se movendo em uma linha reta ao longo do eixo x . Considere que o objeto está na origem em t = 0 . Dos cinco tempos mostrados, qual(is) te
Para cada um dos quatro gráficos de x -versus- t na figura abaixo, responda as seguintes perguntas. (a) A velocidade em t 2 é maior, menor ou igual à velocidade em t 1 ? (b) A rapidez em t 2 é maior,
Um pequeno objeto pesado é largado a partir do repouso e cai por uma distância D em um tempo T . Depois de cair por um tempo 2 T , qual será sua (a) distância de queda a partir da localização inicial,
Você está dirigindo um Porsche que acelera uniformemente de 80,5k m / h ( 50m i / h ) em t = 0,00s até 113k m / h ( 70m i / h ) em t = 9,00s . (a) Qual gráfico na figura abaixo melhor descreve a veloc