Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 23.Exercício - Ex. 30
Para cada um dos seguintes arranjos de duas cargas puntiformes, determine todos os pontos ao longo da linha que passa por ambas as cargas para os quais o potencial elétrico seja igual a zero (suponha V=0 a uma distância infinita das cargas) e para os quais o campo elétrico E seja igual a zero:
a)cargas +Q e +2Q, separadas por uma distância d,
b)cargas -Q e +2Q, separadas por uma distância d.
c)Ambos V e E são iguais a zero nos mesmos pontos? Explique.
Passo 1
Nessa questão a gente precisa descobrir a posição onde o campo E e o potencial V são nulos.
Para isso basta lembramos que:
Passo 2
letra a)
Vamos considerar que as cargas estão separadas por uma distância d e que a posição x é o que queremos obter.
Como as duas cargas são positivas, o potencial total só será nulo no infinito.
Passo 3
Agora para o campo elétrico total no ponto x ser nulo, os campos de cada carga precisam ter mesma intensidade e sentidos opostos
Passo 4
letra b)
Agora as cargas têm sinais contrários!!!!!!!
Ah mas o que isso significa??????
Significa que o potencial zera próximo às cargas!!!!
O potencial será nulo próximo a carga -Q nos pontos A e B.
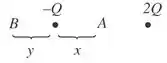
O campo elétrico será nulo à esquerda da carga -Q.
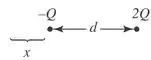
Passo 5
Para calcular o ponto onde o potencial zera, basta a gente usar a relação da letra a.
Como temos dois pontos onde o potencial anula, iremos calcular separadamente.
Ponto A:
Ponto B:
Passo 6
Para o campo total ser nulo, os campos de cada carga precisam ter mesma intensidade e sentidos opostos
Passo 7
letra c)
Vendo os valores que encontramos na letra a e na letra b vemos que e não zeram nos mesmos pontos. Isso porque cai com a distância ao quadrado e decai com a distância.
Resposta
letra a) no infinito , em
letra b) à direita de -Q em e à esquerda de -Q em , à esquerda de -Q em
letra c) Não, por causa da relação deles com a distância.