Uma caixa de , em repouso sobre um chão plano, deve ser deslocada. O coeficiente de atrito estático entre a caixa e o chão é . Uma maneira de deslocar a caixa é empurrá-la com uma força que forma um ângulo abaixo da horizontal. Outro método é empurrá-la com uma força formando um ângulo acima da horizontal. (a) Explique por que um método requer menos força que o outro. (b) Calcule a mínima força necessária para deslocar a caixa de cada maneira, se , e compare os resultados com os resultados para .
Passo 1
Os diagramas para os dois métodos são mostrados abaixo. O método 1 resulta em uma caixa sendo empurrada para o chão, aumentando a força normal e a força de atrito estático. Método 2 parcialmente levanta a caixa, reduzindo a força normal e a força de atrito estático. Podemos aplicar a segunda lei de Newton para obter expressões que relacionam o máximo força de atrito estático ao aplicado força .
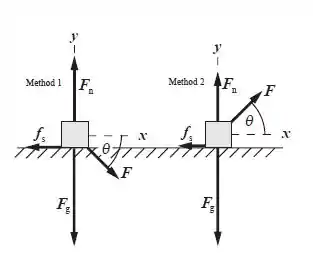
Passo 2
Item (a)
Bem, o melhor método para empurrar a caixa é o método que minimiza a força de atrito. Como a força de atrito é diretamente proporcional a força normal, então o método que tem a menor força normal tem, consequentemente, a menor força de atrito e, portanto, é o método que requer menos esforço. Nesse caso, vemos que o método 2 tem a força normal menor que o método 1, pois a força do método 2 tem uma componente para cima, e como as forças em y tem que se anular (considerando que o bloco não sobe e nem desce), temos , e no método 1, temos . Então, o método que se faz menos esforço para empurrar o bloco é o método 2.
Passo 3
Item (b)
Usando a 2° Lei de Newton no eixo x, temos:
Para o método 1:
Como , temos:
Para o método 2:
Como , temos:
A condição que temos para que o bloco se mova para frente é que a força de atrito máxima , o que faz sentido, pois se o somatório das forças em x for igual a zero, o bloco ou está em repouso ou em movimento uniforme. Então, usando essa condição, chamaremos a força do método 1 de e do método 2 de
Passo 4
Substituindo valores numéricos para e e :
Fazendo o mesmo só que com
Resposta
- o método que se faz menos esforço para empurrar o bloco é o método 2.
- , , ,