Enunciado
Física - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 1.Problemas - Ex. 68
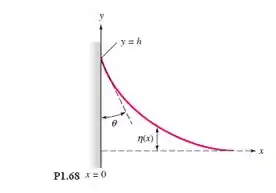
Faça uma análise da forma da interface água-ar próxima de uma parede plana, como na Figura , considerando que a inclinação seja pequena, . Considere também que a diferença de pressão através da interface seja equilibrada pelo peso específico e pela altura da interface, . As condições de contorno são um ângulo de contato molhado em e uma superfície horizontal quando . Qual é a altura máxima na parede?
Passo 1
Vamos lá, essa questão não é nenhuma anomalia, vamos conseguir resolver ela com calma!
Antes de tudo, temos que entender que é um problema bidimensional de tensão superficial e só temos uma curvatura, logo contas mais fáceis! uhul!
Nossa equação diferencial é dada por:
Lembrando que .
Organizando nossa equação temos:
Opa, mas isso é uma EDO de segunda ordem homogênea com uma solução bem conhecida.
Onde:
Caso não se lembre do assunto, nós temos aqui no site! Se for preciso dá uma revisada. :D
Passo 2
Bem agora temos nossa equação, agora temos que descobrir nossas constantes e
Vamos pensar um pouco, se quando , . O termo , deve ser igual a zero, caso contrário , logo.
Agora podemos descobrir para , pois é a altura máxima que o fluído pode atingir.
Assim nossa expressão fica.
Passo 3
Achou que tinha acabado? Achou errado! Kkkk
Tem um último detalhe pra finalizar a questão, a altura máxima! Temos um ângulo de contato que é a famosa reta tangente a curvatura do fluído, assim:
Ilustrando:
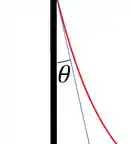
Para :
Isso é tudo pessoal, conseguimos mais uma! \o/
